时间序列预测的顺序

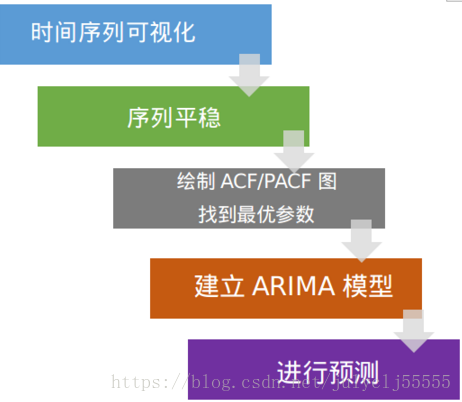
image

时间序列的正式定义如下：它是一系列在相同时间间隔内测量到的数据点。
时间序列的特殊性是：该序列中的每个数据点都与先前的数据点相关。
知乎问答：利用Auto ARIMA构建高性能时间序列模型（附Python和R代码）|source article

#参考文献

常见Markdown公式代码
《时间序列分析》-作者：詹姆斯·D·汉密尔顿（James D.Hamilton）
预测：方法与实践

1 其中常见的时间序列预测算法

1.1 朴素预测法（一次指数平滑）

概念：利用前一时刻的数据，作为下一时刻数据的预测值，公式如下：

$X_{t+1} = X_i$

缺点：那么预测出来的结果会是一条平行线，因为预测结果都是之前的最后一个时刻的值。如下所示：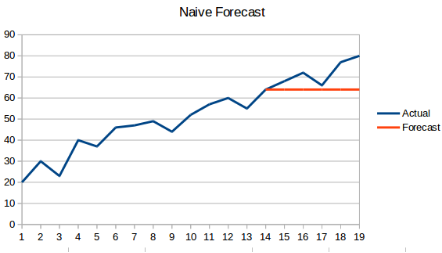
image

1.2 简单平均法

概念：该方法是将之前的所有历史数据进行平均，不再是简单的利用最后一个时刻的数据作为预测值，图像是一条斜线，公式如下：

$X_{t+1} = \frac{1}{N} \sum^N_{i=1} X_i $

where:N表示所有的历史数据的总数.
优点：不像“朴素预测法”那样，直接是一条平行线，该算法中将历史数据也考虑进去；
缺点：但是这些历史数据有些不一定都是有用，所以也会产生一定的误差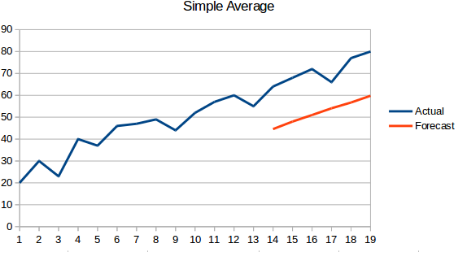
image

1.3 移动平均法

概念：取前n个历史数据的平均，作为下一次的预测结果值，公式如下：

$X_{t+1} = \frac {1}{n} \sum^n_i X_i$

where:n表示前n个数据的数据总数
优点：在朴素预测法和简单平均法的基础上进行改进，使得预测结果更加符合实际
缺点：最接近下一时刻的数据与下一时刻的真实数据明显更加接近，没有考虑权重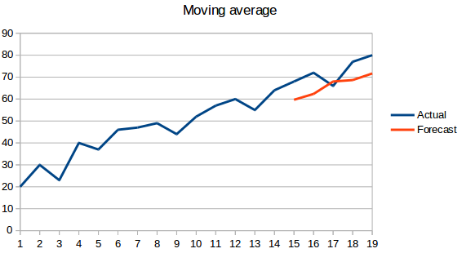
image

1.4 加权移动平均法

概念：在移动平均法的基础上，对前n个数据给予不同的权重，那么对下一时刻的预测结果将更加接近真实值，公式如下：

$X_{t+1} = \frac {1}{n} \sum^n_i X_i \cdot W_i$

where:W表示每个数据点的权重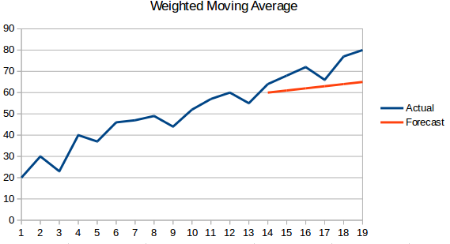
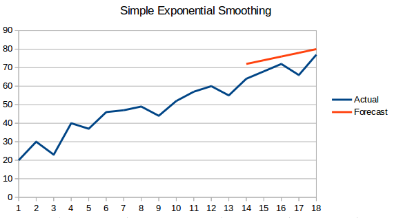
image

1.5 简单指数平均法

概念：在该方法中，同样取前n个数据的平均同时加权重，但是更近期的观测结果会被赋予更大的权重，公式如下：

$X_{t+1} = \frac {1}{n} \sum^n_i X_i \cdot W_i 且W_i>W_{i-1}$

image

1.6 霍尔特（Holt）线性趋势预测

概念：在之前的基础上，该方法加入了数据集的趋势，也就是数据的整体上涨或下跌等。
优点：该方法能够按照一定的趋势去预测，而不是盲目的预测，结果更具说服性
缺点：该方法只考虑了趋势性（上涨或下跌），但是没有考虑数据的季节性，也就是数据集的周期性。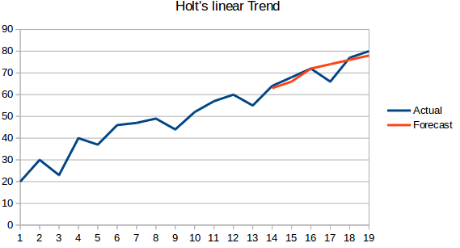
image

1.7 霍尔特-温特斯（Holt Winters）方法（三次指数平滑）

概念：该方法在霍尔特线性趋势预测的基础上了，加入了季节性，也就是说，该方法同时具有趋势性和季节性。

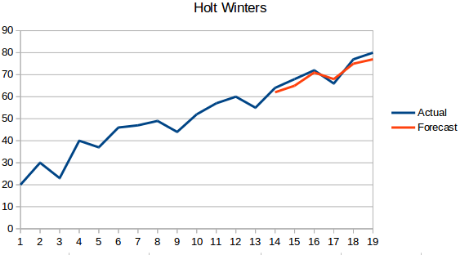
image

指数平滑法

指数平滑法有几种不同形式：一次指数平滑法针对没有趋势和季节性的序列，二次指数平滑法针对有趋势但没有季节性的序列，三次指数平滑法针对有趋势也有季节性的序列。“Holt-Winters”有时特指三次指数平滑法。

2.1 MSE-均方误差(mean square error)

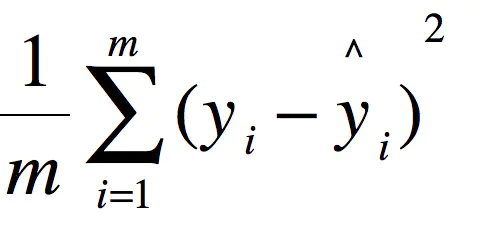
image
这里的y是测试集上的。
用 真实值-预测值 然后平方之后求和平均。

2.2 RMSE-均方根误差(root mean square error)

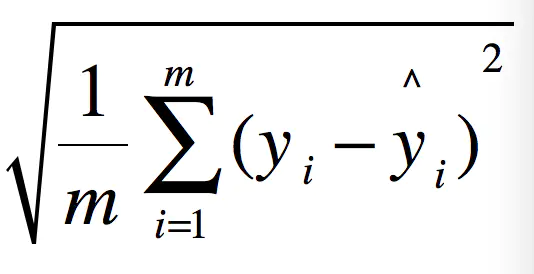
image

例如：要做房价预测，每平方是万元（真贵），我们预测结果也是万元。那么差值的平方单位应该是 千万级别的。那我们不太好描述自己做的模型效果。怎么说呢？我们的模型误差是 多少千万？。。。。。。于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的可，在描述模型的时候就说，我们模型的误差是多少万元。

2.3 MAE-平均绝对误差(mean absolute error)

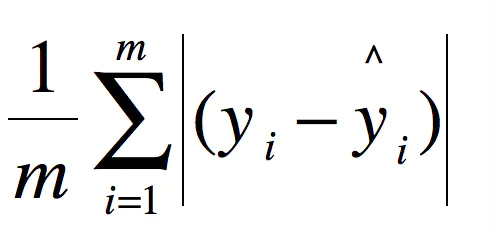
image

2.4 R Squared

为了能够让模型有一个标准的衡量标准，这里引入R方的概念。

比如说预测房价 那么误差单位就是万元。数子可能是3，4，5之类的。那么预测身高就可能是0.1，0.6之类的。没有什么可读性，到底多少才算好呢？不知道，那要根据模型的应用场景来。
看看分类算法的衡量标准就是正确率，而正确率又在0～1之间，最高百分之百。最低0。很直观，而且不同模型一样的。那么线性回归有没有这样的衡量标准呢？答案是有的。
那就是R Squared也就R方

公式：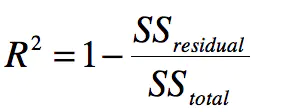
image
其中分子是Residual(残差) Sum of Squares 分母是 Total Sum of Squares

慢慢解释。其实这个很简单：

  • 上面分子就是我们训练出的模型预测的所有误差。
  • 下面分母就是不管什么我们猜的结果就是y的平均数。（瞎猜的误差）

结果如下：

  • 如果结果是0，就说明我们的模型跟瞎猜差不多。
  • 如果结果是1。就说明我们模型无错误。
  • 如果结果是0-1之间的数，就是我们模型的好坏程度。
  • 如果结果是负数。说明我们的模型还不如瞎猜。（其实导致这种情况说明我们的数据其实没有啥线性关系）

公式的分子分母同时处以m，得：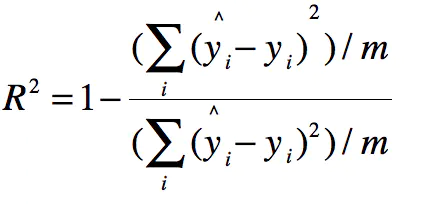
image

那么分子便成了MSE，分母就是方差，有如下：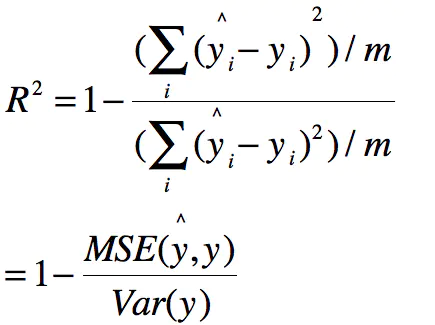
image

补充：什么是方差？
方差（英语：Variance），应用数学里的专有名词。在概率论和统计学中，一个随机变量的方差描述的是它的离散程度，也就是该变量离其期望值的距离。一个实随机变量的方差也称为它的二阶矩或二阶中心矩，恰巧也是它的二阶累积量。这里把复杂说白了，就是将各个误差之平方（而非取绝对值，使之肯定为正数），相加之后再除以总数，透过这样的方式来算出各个数据分布、零散（相对中心点）的程度。继续延伸的话，方差的正平方根称为该随机变量的**标准差（此为相对各个数据点间），方差除以期望值归一化的值叫分散指数，标准差除以期望值归一化的值叫变异系数**。

3 循环神经网络

循环神经网络（Recurrent Neural Network）是一种基于序列结构数据的神经网络模型，在处理时间序列数据时，具有一定的优势。在RNN模型中，下一层的隐含层的输入是前一层隐含层的输入，这样做的目的就是为了能够“记住”整个序列的数据，从而能够对一些有时间顺序的数据进行处理。但是RNN也有缺点，缺点也由于其“优势”所导致的，在利用BPTT（Back Propagation Through Time，基于时间的反向传播）算法优化参数时，可能会遇到梯度消失（或者说梯度弥散）或者梯度爆炸的问题。由于BPTT的本质也是采用逐层梯度下降，然而梯度下降也就是求偏导数，如果每层的偏导数都小于1，那么就会出现梯度消失；反之，如果每层的偏导数大于1，那么就会出现梯度爆炸。
公式如下：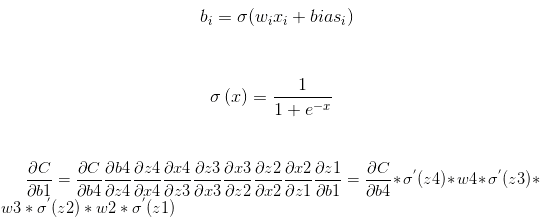
image
RNN的结构如下：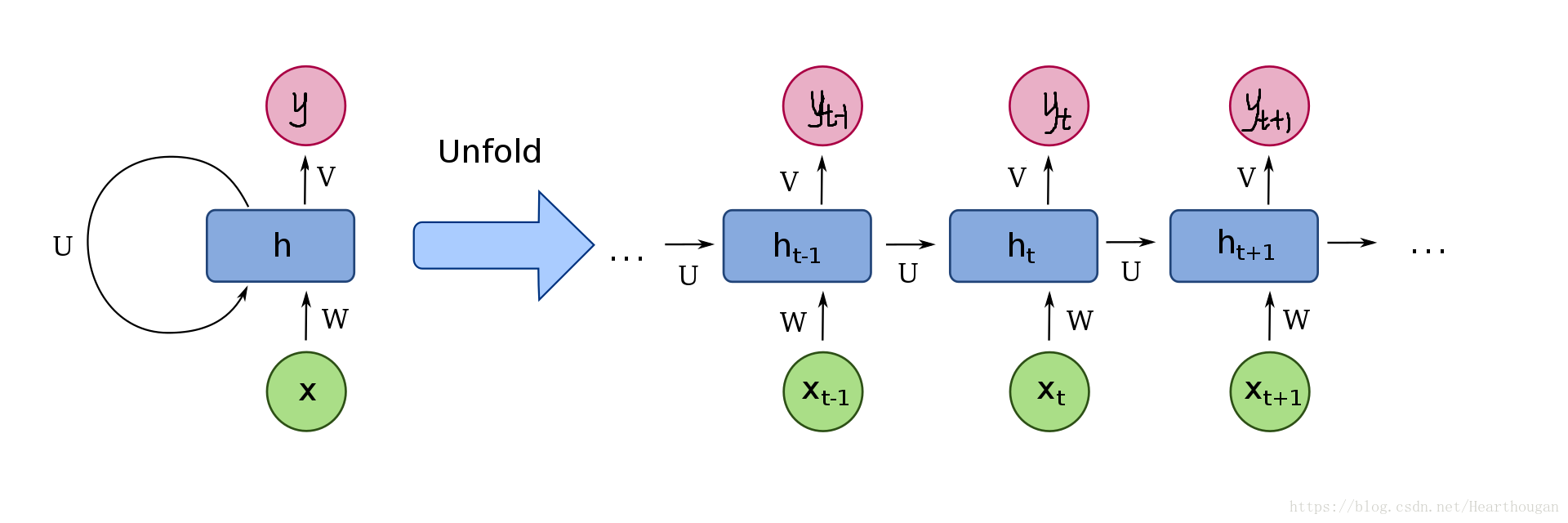
image

（1） 梯度爆炸的解决方法

  • 重新设计网络结构
  • 使用激活函数（ReLU函数等）
  • 使用权重正则化
  • 使用梯度剪枝
  • LSTM

（2） 梯度消失的解决办法

由于梯度消失的问题比较棘手，不像梯度爆炸那样比较容易解决，需要对原网络进行改进，在此基础上，有诞生了

  • GRU（Gate Recurrent Unit），门循环单元
  • LSTM（Long Short Term Memory）,长短时记忆网络。

3.1 长短时记忆网络

为了解决基础RNN中出现的梯度消失和梯度爆炸问题，LSTM（Long Short Term Memory）于1997年被提出，且能很好的解决RNN中的梯度消失和梯度爆炸问题。

（1）LSTM介绍

概念：

  • 一个LSTM Cell是由3个门限结构和1个状态向量传输线组成的，门限分别是遗忘门，传入门，输出门；
  • 其中状态向量传输线负责长程记忆，因为它只做了一些简单的线性操作；3个门限负责短期记忆的选择，因为门限设置可以对输入向量做删除或者添加操作;

下图是RNN和LSTM的结构图比较，右侧为LSTM：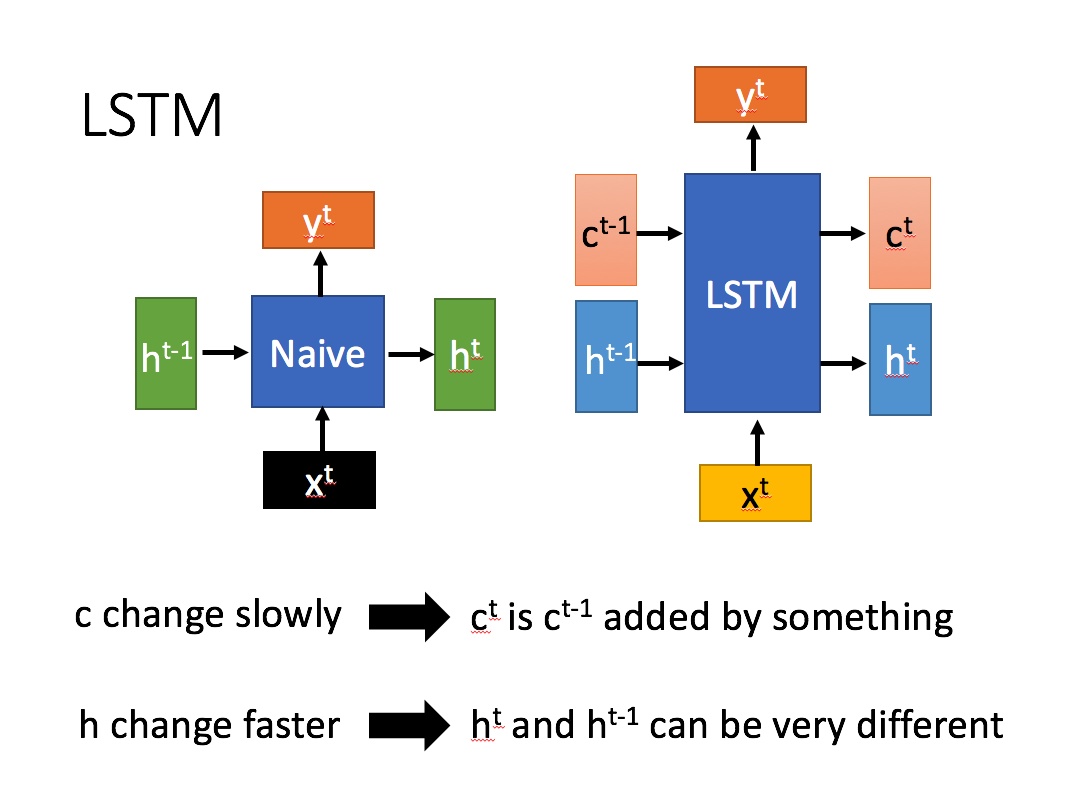
image

左侧：
其中$x^t$表示的是当前t时刻的输入， $h^{t-1}$表示的是上一时刻的隐含层输出值， $h^t$表示的是t时刻隐含层状态， $y^t$表示的是当前$t$时刻的输出值，Naive表示的是普通的RNN。

LSTM中的参数介绍：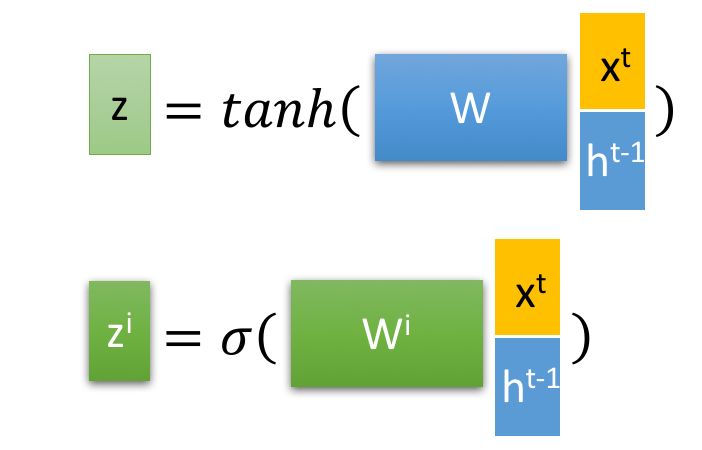
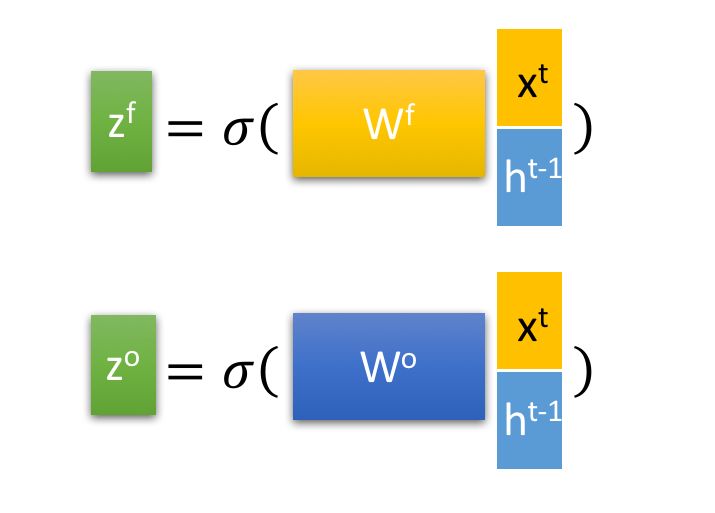
image
image

LSTM的内部结构：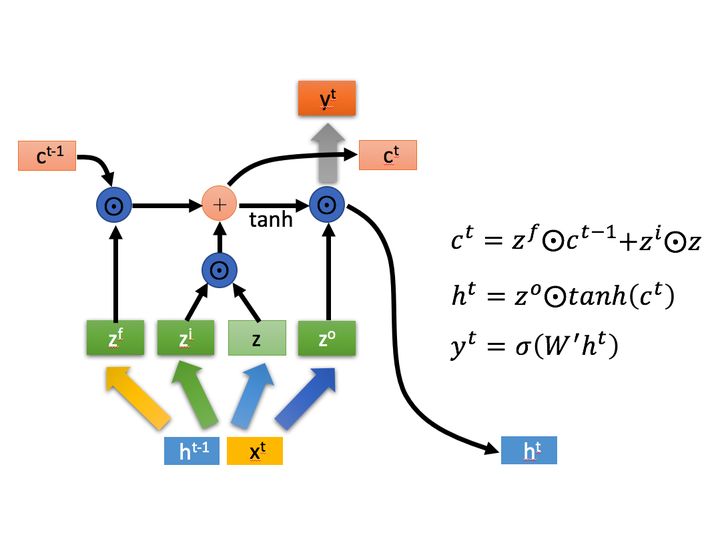
image

多层LSTM的连接结构：
以下是一个LSTM cell结构图：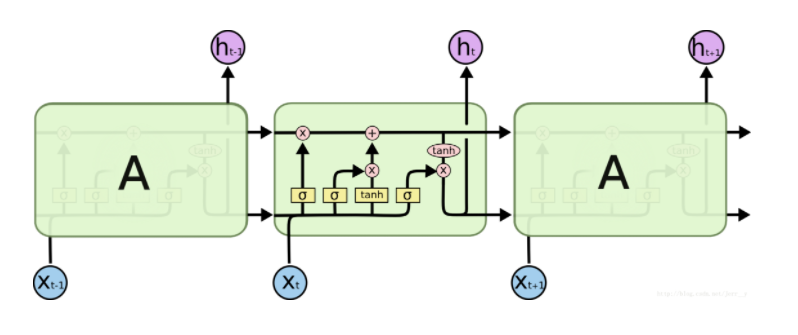
image

1）遗忘门
遗忘门是通过一个sigmoid函数来实现，“0”表示决绝任何输入，“1”表示接受所有输入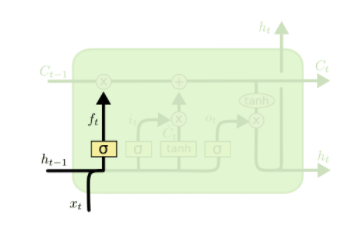
image

2）输入门（选择记忆）
输入门有两部分组成，一部分是由sigmoid函数来决定哪些信息需要更新，一部分由tanh函数来生成一个备选的用来更新的内容；然后再将这两部分进行向量点乘。
作用：决定让多少新的信息加入到cell状态中来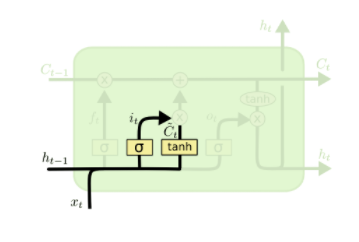
image

3）输出门
该部分同样由两部分构成，一部分由sigmoid函数决定哪些信息需要输出，接着，另一部分是把一个状态向量通过一个tanh层（tanh函数），然后把tanh的状态输出和由sigmoid函数计算出来的权重相乘。这就得到了最后的结果。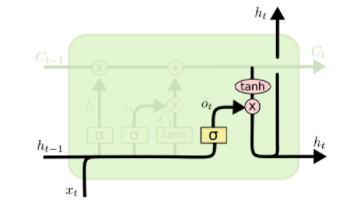
image

4）状态更新
首先由旧的状态和遗忘门的输出相乘，把一些不想保留的信息忘掉，然后加上输入门的输出，这部分信息就是我们想要新添加的内容

（2）LSTM的优缺点介绍
  • 优点
    • 解决了RNN中的梯度消失和梯度爆炸问题
  • 缺点
    • 计算速度较慢

3.2 GRU

针对LSTM的缺点（计算速度偏慢），门控循环单元（Gate Recurrent Unit，GRU）在2014年被提出，在LSTM结构的基础上，GRU进行了改进。相比于LSTM，GRU减少了一个“门控单元”。在LSTM中有三个“门控单元”，分别是遗忘门、输入门、输出门来控制输入值、记忆值和输出值。而GRU中之后更新门(z)和重置门(r)两个“门控单元”，少了一个“门控单元”，其计算复杂度降低了，运行速度也提升了。

（1）GRU的结构介绍

GRU的内部结构图：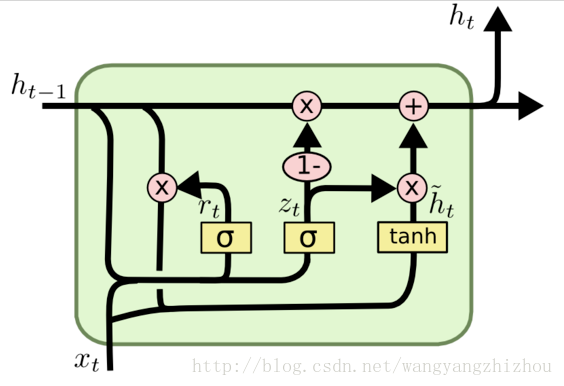
image

GRU的状态图：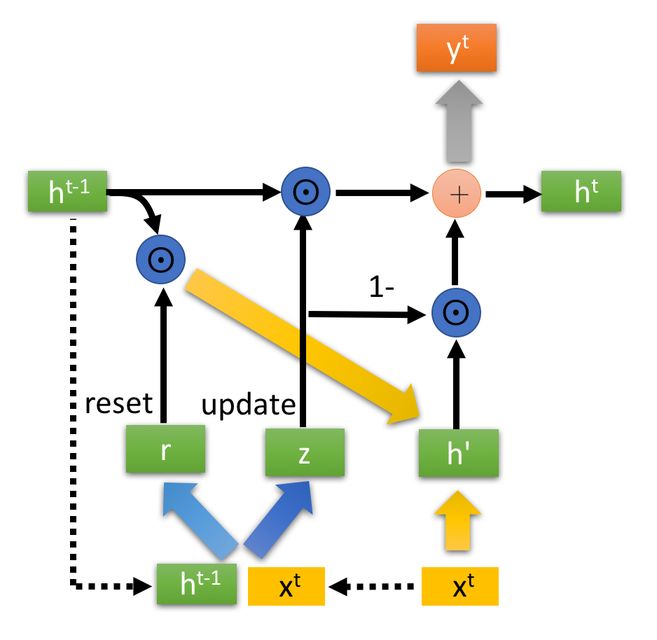
image

GRU的两个门控：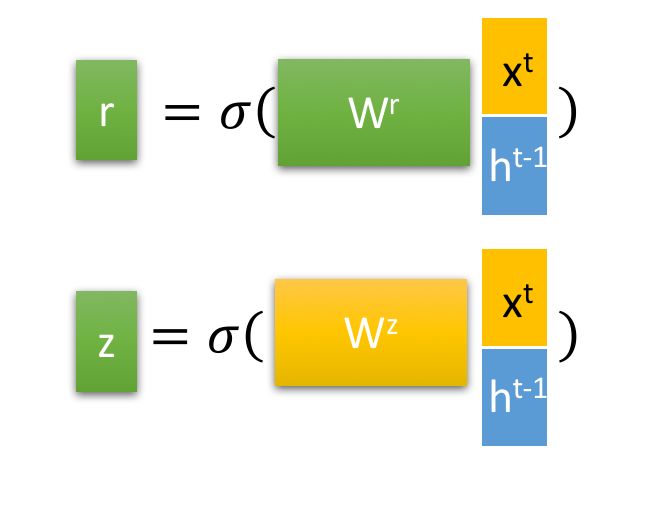
image
首先再次强调一下，门控信号（这里的z ）的范围为0~1。门控信号越接近1，代表”记忆“下来的数据越多；而越接近0则代表”遗忘“的越多。

（2）GRU和LSTM的关系

我们知道GRU也是RNN的一种，且GRU是LSTM的一个变种或者说是简化版，但是他们之间的关系其实是：GRU利用更新门(z)代替了LSTM中的遗忘门和输入门，更新门既可以进行“遗忘”也可以进行“选择记忆”，这一点由更新表达式可以看出。

RNN的参考文献

深度学习之RNN(循环神经网络)
人人都能看懂的GRU
人人都能看懂的LSTM
一文了解LSTM和GRU背后的秘密（绝对没有公式）
循环神经（LSTM）网络学习总结摘要
什么是白噪声？如何判断时间序列是白噪声？
时间序列分析——自回归移动平均（ARMA）模型
时间序列模式（ARIMA）—Python实现

4 奇异谱分析（SSA）

奇异频谱分析（Singular spectral analysis，SSA）

5 自回归移动平均（ARMA）

AR（p）,MA（q）
因为AR（p）,MA（q）,ARMA（p,q）都是平稳随机过程，对于有些时间序列数据不能很好的进行预测，比如有些数据在时间上具有季节性和或趋势性，像这样非平稳随机过程ARMA不能很好的预测，所以引入ARIMA（差分自回归移动平均），即在p,q两个参数的基础上，再加一个将时间序列变为平稳时所做的差分次数d。

什么是平稳随机过程？

平稳随机过程就是该随机过程的统计特性不随时间的推移而产生变化，因此其数学期望和方差都不变。

#ARMA参考文献

AR,MA->ARMA->ARIMA

6 差分自回归移动平均（ARIMA）

差分自回归移动平均模型（Auto Regressive Integrated Moving Average Model ,简称ARIMA）。|MBA智库-解释
AR是（Auto Regressive）自回归，p是自回归项；MA（Moving Average）是移动平均，q是移动平均项；d是时间序列成为平稳时所做的差分次数。
ARIMA模型的提出是为了解决ARMA模型不能预测非随机平稳过程的问题，ARIMA的思路是：现将给定的非平稳随机过程转换成平稳随机过程，然后再使用ARMA模型进行预测。

7 支持向量回归（SVR）

支持向量回归（Support Vector Regression），SVM的英文全称是Support Vector Machines，中文叫支持向量机。支持向量机是我们用于分类的一种算法。支持向量也可以用于回归，所以叫支持向量回归。

8 三次指数平滑

8.1 为什么叫“指数平滑”？

先看公式：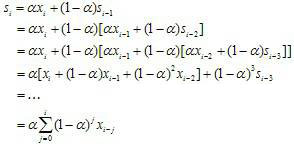
image
从公式中可以看出，该算法对整个时间序列中的数据多进行了计算，但是时间越久远，其对下一时刻的影响越小，指数越大，其权重越小。

8.2 算法优点

该算法考虑了时间序列的趋势性和季节性。

#三次指数平滑参考文献

时间序列挖掘-三次指数平滑法(Holt-Winters)

什么是白噪声？

纯随机序列，也称为白噪声序列，序列的各项之间没有任何的关系， 序列在进行完全无序的随机波动， 可以终止对该序列的分析。
当时间序列预测模型的预测达到了白噪声时，那么该模型就类似于收敛了。

机器学习模型中的参数和超参数的区别？

参数：是模型内部的参数，是模型从历史数据中“学习”到的参数，比如W和b，其值可以通过数据估计然后模型训练得到
超参数：是不能从模型中得到的参数，可以理解为模型外的参数，其值不能从数据估计得到
参考文件：机器学习中模型参数与超参数的区别

机器学习模型中的训练集、校验集、测试集

  • 训练集：用于训练模型，找出最佳的w和b。
  • 验证集：用以确定模型超参数，选出最优模型。
  • 测试集：仅用于对训练好的最优函数进行性能评估。

参考文献：https://blog.csdn.net/hohaizx/article/details/81013985

写在最后

欢迎大家关注鄙人的公众号【麦田里的守望者zhg】，让我们一起成长，谢谢。
微信公众号