环形链表问题

crazyjums

LeetCode刷题链表middle

发布于：Nov 13, 2020

次浏览

141. 环形链表

https://leetcode-cn.com/problems/linked-list-cycle/

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

示例 1：

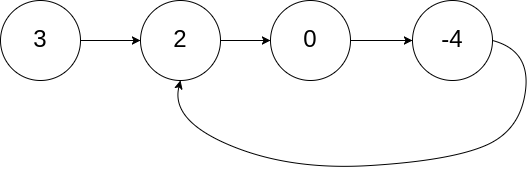
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：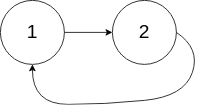

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 $[0, 104]$
$-105 <= Node.val <= 105$
$pos$ 为$ -1$ 或者链表中的一个有效索引。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/linked-list-cycle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

1 解题思路

想象一下这种场景：在足球场上，甲和乙在进行跑步比赛，已知甲和乙的速度恒定不变，且甲的速度是乙的两倍，假设乙的速度是$v$，则甲的速度是$2v$。他们在同一时刻起跑，那么最后总有这么一个时刻，甲能追上乙，即甲乙相遇。

此问题和上面的场景有点像，那么我们只需要制造甲和乙，并且指定他们的速度就可以。可以使用快慢指针$slow$、$fast$，如果链表中存在环，那么这两个指针最终一定可以相遇，即$slow==fast$。如果他们最后相等了，那么说明有环，否则说明没有。代码如下。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head==null) return false;
        
        ListNode slow = head;
        ListNode fast = head;
        
        while(fast!=null && fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
            if(slow == fast)
                return true;
        }
        return false;
    }
}

2 题目进阶

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

进阶：

你是否可以使用 O(1) 空间解决此题？

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

链表中节点的数目范围在范围 $[0, 104]$内
$-105 <= Node.val <= 105$
$pos$ 的值为$ -1$ 或者链表中的一个有效索引

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/linked-list-cycle-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

此题目是在上一题的基础上的改进，即如果链表中存在环，那么求出环的入口节点并返回该入口节点。

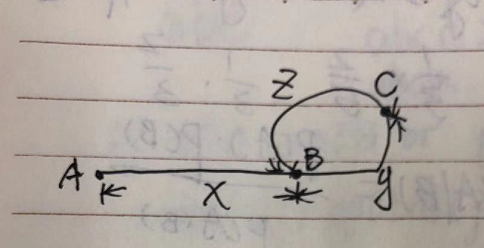
假设端点$A$是链表的起始点，端点$B$是链表中环的入口节点，端点$C$是快慢指针相遇的节点，由于快指针$fast$的移动速度是慢指针$slow$的两倍，所以可以知道快指针所走过的路径是慢指针所走过的路径的两倍。看图可以知道，慢指针所走过的路径是：$x+y$；快指针所走过的路径是：$x+y+y+z$，即$x+z+2y$。则有$2(x+y)=x+z+2y$，化简后的$x=z$。

根据以上推理过程，可以知道$x$和$z$的长度一样的，那么当快慢指针相遇之后，可以将快慢指针中的某个指针移动到链表头部，此时让快慢指针以相同的速度向前进，他们最终一定会在$B$点相遇，那么$B$点就是环的入口节点。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null) return null;
        ListNode s = head;
        ListNode f = head;
        while (f != null && f.next != null) {
            s = s.next;
            f = f.next.next;
            if (s == f) 
                break;
        }
        f = head;
        while (f != s && s != null) {
            s = s.next;
            f = f.next;
        }
        return s;
    }
}