CrazyJums LeetCode and Pary For Good Job

首页

归档

看书

CSDN

算法

GitHub

6道回溯算法题，了解以及掌握回溯法的基本套路

crazyjums
LeetCode刷题算法总结回溯法

发布于：Nov 15, 2020

次浏览

46. 全排列

https://leetcode-cn.com/problems/permutations/

46. 全排列

https://leetcode-cn.com/problems/permutations/

47. 全排列 IIhttps://leetcode-cn.com/problems/permutations-ii/

https://jums.club/leetcode/images/safari.png

78. 子集

https://leetcode-cn.com/problems/subsets/

90. 子集 II

https://leetcode-cn.com/problems/subsets-ii/)

39. 组合总和

https://leetcode-cn.com/problems/combination-sum/

40. 组合总和 II

https://leetcode-cn.com/problems/combination-sum-ii/

1 使用回溯算法求46. 全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

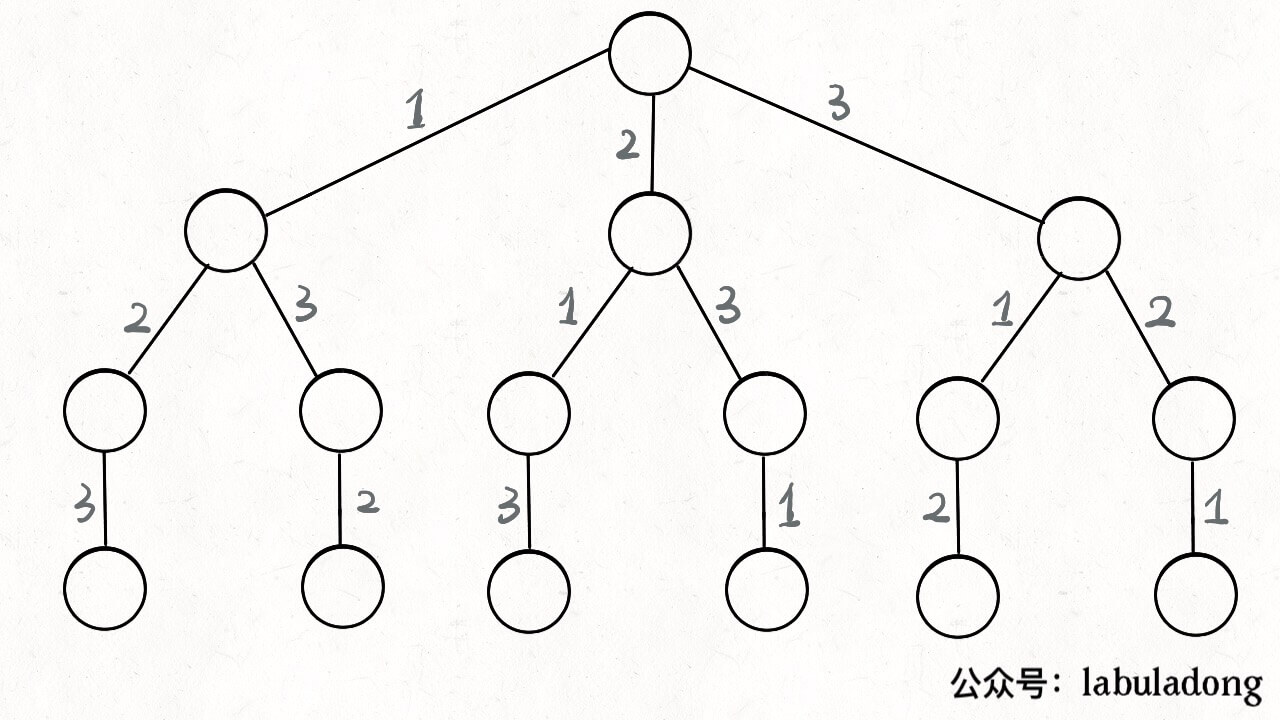
这是一道金典的回溯算法题，使用回溯法进行求解，我们通过在这道题来了解什么是回溯，以及掌握回溯算法的套路。回溯即重新回过头去看的意思，也就是说使用该方法进行求解时，需要不时的回头看看，我们可以画出该题的回溯树，从下面的回溯树可以看出，回溯法的求解过程类似于深度优先搜索。这里需要注意几个地方，即数组中的元素用过一次之后，不能再之后的选择中再次出现。比如第一个分支，选择了$1$之后，后面的两个分支就只能选择$2$或者$3$。其他两个分支也是类似，那么就需要一个有这么一个数据结构能够记录当前所做出的选择，并在回溯之后撤销当前所做的选择。这里我们可以使用一个相同大小的数组即可，每次做出选择时，在相同的下标位置做上标记，当回溯到上一层时，消除标记，为了判断时方便，这里使用$boolean$型数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        if (nums == null || nums.length == 0) {
            return res;
        }
        List<Integer> path = new ArrayList<>();
        boolean[] used = new boolean[nums.length]; //也可以使用int或者其他类型的数组，只要能标记就行
        dfs(used, res, path, nums);
        return res;
    }

    private void dfs(boolean[] used, List<List<Integer>> res, List<Integer> path, int[] nums) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (!used[i]) {
                path.add(nums[i]);
                used[i] = true;
                dfs(used, res, path, nums);
                used[i] = false;
                path.remove(path.size() - 1);
            }
        }
    }
}

2 回溯算法的解题模板

通过上面的题，我们应该能大概知道回溯算法的一个解题思路，通常遇到一道回溯算法题时，首先应该在抄稿纸上画出该题的回溯树，如果需要剪枝的话，还需要进行剪枝操作，这里我们可以通过47. 全排列 II这一题了解回溯法的剪枝过程。回溯算法的大致模板如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();  //1、定义结果集的容器
        if (nums == null || nums.length == 0) { //2、判断条件下的结果
            return res;
        }
        List<Integer> path = new ArrayList<>(); //3、定义单个的回溯路径容器
        boolean[] used = new boolean[nums.length]; //4、定义标记数据结构，用于防止重复访问，这是非必要
        dfs(used, res, path, nums); //5、进入回溯算法的递归树中
        return res; //返回最终结果
    }

    private void dfs(boolean[] used, List<List<Integer>> res, List<Integer> path, int[] nums) {
        if (path.size() == nums.length) { // 1、定义递归的退出条件，必须有 当回溯路径中取到所有选择时，则添加到结果集并退出递归
            res.add(new ArrayList<>(path));
            return; // 必须要返回
        }

        for (int i = 0; i < nums.length; i++) { // 2、当前逻辑  即做出选择，一共有多少种选择
            if (!used[i]) { //该步是判断当前的元素是否已经被选择过，如果没有，则需要进一步做选择，否则跳过
                path.add(nums[i]); //3、将当前的选择添加到回溯分支中
                used[i] = true; //并标记当前选择已经被选择过，在当前的回溯分支中该元素不能再被重新选择
                dfs(used, res, path, nums); // 4、当前选择已经做好了，继续向下左选择，进入下一个回溯分支
                used[i] = false; //5、如果下一个分支到头了，即到了回溯树的叶子节点处，此时即找到了一个结果，将其添加到结果集中，并向上回溯一层，即撤销当前的选择，慢慢想回溯树的根部移动，回溯到上一层后，需要撤销当前所做的选择
                path.remove(path.size() - 1); //回溯一层后，需要将当前的回溯分支的叶子部分进行删除
            }
        }
    }
}

上面是在46. 全排列的代码基础上进行的一个分析，下面给出一个抽象的模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public 结果集容器 方法名(选择列表) {
        1、定义结果集容器;
        2、判断特殊情况下的结果;
        3、定义一个存放回溯分支的容器;
        4、进入回溯函数，这里定义为backTrack();
        return res;   
    }
    
    private void backTrack(res, path, nums) {
        1、递归退出条件;
        
        2、定义当前逻辑;
        for (num : nums) { //列出所有的可能选择
            //如果需要，可以判断当前选择是否在之前已经被选择过;
            path.add(num); //将当前的选择添加到回溯的分支中，当前选择必须是可以被选择的一个选择
            //继续进入下一层的回溯分支
            backTrack(res, path, nums);
            //撤销上一层所做的选择，
            path.remove(path.size() - 1);
        }
    }
}

3 回溯算法的剪枝-47. 全排列 II

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

该题是在全排列的基础上进行了改进，这里的选择中可能会出现重复的元素，但是结果集中不能有重复的解，那么使用上一题的解法定义一个标记数组来解这道题的话，也可以解出来，然后在添加到结果集中时判断一下当前的回溯分支是否已经在结果集中，如果不在，则添加，否则不添加，但是这样会出很多的无畏的操作，导致算法的时间复杂度很高。

  • 在添加到结果集中之前，需要判断当前的回溯分支是否在结果集中，这一步的时间复杂度是$O(n)$
  • 由于回溯树做了很多无畏的计算，那么这一步的最坏的时间复杂度是$O(2^n)$

下图来自力扣题解。

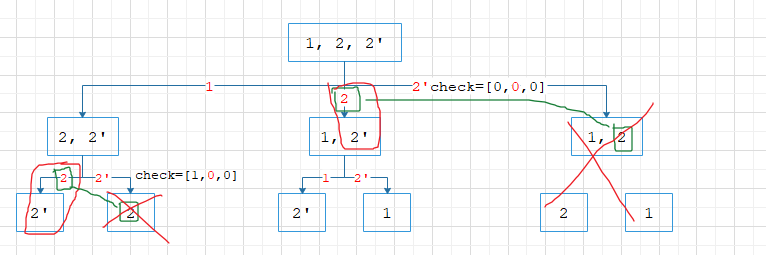
从上图可以看出，第二层的第三个分支被剪枝了，也就是这一个分支没有参与计算，这样就大大减小了回溯树的时间复杂度。那么我们没必要在添加到总的结果集中时才判断当前回溯是否重复，我们可以可以在回溯搜索的时候就判断，即上图中的剪枝操作，我们可以先对选择数组进行排序，然后在回溯的过程中：

  • 如果是第一个待选择的选择，我们不需要判断，直接添加即可
  • 如果是第二个待选择的选择时，先判断当前选择的前一个选择是否被选择过以及是否和当前的选择相等，如果和当前的选择相等的话，那么在往下的回溯分支就会和上一个的回溯分支重复，这就不符合题意，所以这一步跳过即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        if (nums == null || nums.length == 0) 
            return res;
        List<Integer> path = new ArrayList<>();
        boolean[] used = new boolean[nums.length];
        Arrays.sort(nums);
        dfs(res, path, used, nums);
        return res;
    }

    private void dfs(List<List<Integer>> res, List<Integer> path, boolean[] used, int[] nums) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            /**
            * 可以将此思路当成是由nums.length个空格，从nums数组中选择数字填到这些空格中，
            * 从左往右，在填右边这个元素时，要先判断一下左边的元素是否被用过，如果没有被用过，那
            * 左边的元素是否和右边待填的元素相等，如果想等，也不能填
            */
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) { //从第二个选择开始判断是否剪枝
                continue;
            }
            if (!used[i]) {
                path.add(nums[i]);
                used[i] = true;
                dfs(res, path, used, nums);
                path.remove(path.size() - 1);
                used[i] = false;
            } 
        }
    }
}

4 回溯剪枝的模板

回溯算法的剪枝，必须对选择数组进行排序，否则不可能实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public 结果集容器 方法名(选择列表) {
        1、定义结果集容器;
        2、判断特殊情况下的结果;
        3、定义一个存放回溯分支的容器;
        4、进入回溯函数，这里定义为backTrack();
        return res;   
    }
    
    private void backTrack(res, path, nums) {
        1、递归退出条件;
        
        2、定义当前逻辑;
        for (int i = 0; i < nums.length; i++) { //列出所有的可能选择
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])  //从第二个选择开始判断是否剪枝
                continue; //剪枝
            //如果需要，可以判断当前选择是否在之前已经被选择过;
            path.add(num); //将当前的选择添加到回溯的分支中，当前选择必须是可以被选择的一个选择
            //继续进入下一层的回溯分支
            backTrack(res, path, nums);
            //撤销上一层所做的选择，
            path.remove(path.size() - 1);
        }
    }
}

5 其他与该题类似的回溯算法题

78. 子集

https://leetcode-cn.com/problems/subsets/

该题除了可以使用回溯算法解题之外，还可以结合二进制和迭代进行解题。这里只列出回溯法的，有兴趣的可以自己想想怎么用二进制求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        int m = 1 << n;
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        dfs(res, path, 0, nums);
        return res;
    }
    //index表示当前查到所有选择中的第几个选择
    private void dfs(List<List<Integer>> res, List<Integer> path, int index, int[] nums) {
        if (nums.length < index) { 
            return;
        }
        res.add(new ArrayList<>(path)); //由于是求子集，所以是每一个回溯都是全集的自己
        for (int i = index; i < nums.length; i++) {
            path.add(nums[i]);
            dfs(res, path, i + 1, nums);
            path.remove(path.size() - 1);
        }
    }
}

90. 子集 II

https://leetcode-cn.com/problems/subsets-ii/)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        Arrays.sort(nums);
        dfs(res, path, 0, nums);

        return res;
    }

    private void dfs(List<List<Integer>> res, List<Integer> path, int index, int[] nums) { 
        if (index > nums.length)
            return;

        res.add(new ArrayList<>(path)); //同样
        for (int i = index; i < nums.length; i++) {
            if (i > index && nums[i] == nums[i - 1]) continue;

            path.add(nums[i]);
            dfs(res, path, i + 1, nums);
            path.remove(path.size() - 1);
        }
    }
}

39. 组合总和

https://leetcode-cn.com/problems/combination-sum/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        Arrays.sort(candidates); //排序的目的是为了剪枝
        dfs(candidates, target, 0, 0, res, path);
        return res;
    }

    private void dfs(int[] candidates, int target, int sum, int index, List<List<Integer>> res, List<Integer> path) {
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = index; i < candidates.length; i++) {
            int rs = sum + candidates[i];
            if (rs <= target) {
                path.add(candidates[i]);
                dfs(candidates, target, rs, i, res, path);
                path.remove(path.size() - 1);
            } else { //剪枝 大于target的部分可以剪枝
                break;
            }
        }
    }
}

40. 组合总和 II

https://leetcode-cn.com/problems/combination-sum-ii/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        Arrays.sort(candidates);
        dfs(res, path, candidates, target, 0, 0);
        return res;
    }

    private void dfs(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int index) {
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = index; i < candidates.length; i++) {
            if (i > index && candidates[i] == candidates[i - 1])
                continue;
            int rs = sum + candidates[i];
            if (rs <= target) {
                path.add(candidates[i]);
                dfs(res, path, candidates, target, rs, i + 1);
                path.remove(path.size() - 1);
            } else {
                break;
            }
        }
    }
}
相关文章
514. 自由之路514. 自由之路， https://leetcode-cn.com/problems/freedom-trail/htt...打家劫舍198. 打家劫舍https://leetcode-cn.com/problems/house-robber/18.四数之和18. 四数之和https://leetcode-cn.com/problems/4sum/环形链表问题141. 环形链表https://leetcode-cn.com/problems/linked-list-cycle/

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：http://jums.club/back-tracks/

更新于：Nov 15, 2020

LeetCode刷题

算法总结

回溯法

评论