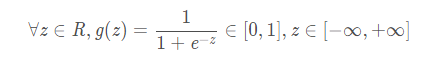学习计算机视觉，你必须了解的基础概念

1 图像的高频和低频成分

形象一点说：亮度或灰度变化激烈的地方对应高频成分，如边缘；变化不大的地方对于低频成分，如大片色块区画个直方图，大块区域是低频，小块或离散的是高频把图像看成二维函数，变化剧烈的地方就对应高频，反之低频。
举个通俗易懂的例子：
一幅图象，你戴上眼镜，盯紧了一个地方看到的是高频分量
摘掉眼镜，眯起眼睛，模模糊糊看到的就是低频分量。
图像的高低频是对图像各个位置之间强度变化的一种度量方法.
低频分量:主要对整副图像的强度的综合度量.
高频分量:主要是对图像边缘和轮廓的度量.
如果一副图像的各个位置的强度大小相等,则图像只存在低频分量,从图像的频谱图上看,只有一个主峰,且位于频率为零的位置.
如果一副图像的各个位置的强度变化剧烈,则图像不仅存在低频分量,同时也存在多种高频分量,从图像的频谱上看,不仅有一个主峰,同时也存在多个旁峰.
以上的现象可以通过对傅里叶变换的公式分析得出.
以下所说的积分是对x进行的.
exp(-jwx)的数值变化是均匀的,如果对exp(-jwx)进行积分,则积分值为零.如果对exp(-jwx)乘以一个加权函数f(x),则在对f(x)exp(-jwx)进行积分,积分值不一定为零.如果exp(-jwx)的取值为1时,则对f(x)exp(-jwx)积分,既为对f(x)积分,此时f(x)exp(-jwx)最大,既频谱中的主峰.如果f(x) 是常数则, 除w=0处f(x)exp(-jwx)的积分不为零外,在w不为零的其它处,f(x)exp(-jwx)的积分都为零.

2 低通滤波

低通滤波(Low-pass filter) 是一种过滤方式，规则为低频信号能正常通过，而超过设定临界值的高频信号则被阻隔、减弱。但是阻隔、减弱的幅度则会依据不同的频率以及不同的滤波程序（目的）而改变。它有的时候也被叫做高频去除过滤（high-cut filter）或者最高去除过滤（treble-cut filter)。低通过滤是高通过滤的对立。

3 bounding-box

如图所示，绿色的框为飞机的Ground Truth，红色的框是提取的Region Proposal。那么即便红色的框被分类器识别为飞机，但是由于红色的框定位不准(IoU<0.5)，那么这张图相当于没有正确的检测出飞机。如果我们能对红色的框进行微调，使得经过微调后的窗口跟Ground Truth更接近，这样岂不是定位会更准确。确实，Bounding-box regression 就是用来微调这个窗口的。

R-CNN的论文原文是《Rich feature hierarchies for accurate object detection and semantic segmentation》全是英文，有兴趣的可以读一读
R-CNN是计算机视觉中目标检测算法的鼻祖，很多的目标检测算法都是基于R-CNN的改进，这里有一篇很好的博客，介绍了R-CNN,Fast R-CNN,Faster R-CNN的一个工作原理
B站目标检测大牛
关于R-CNN的一个入门视频

R-CNN的工作原理：

R-CNN利用网络将特征提取和特征分类合并到一起，大大提升了特征的提取效率。但是无论是传统方式还是R-CNN，目标检测和目标识别的最大区别就是需要提取候选区域（region proposals） R-CNN采用选择性搜索（selective search）算法，又称区域合并算法，selective search会将对图片暴力生成多个候选区域

R-CNN算法的计算过程：

首先输入图像会被分为R个初始候选集，

然后通过贪心策略去计算相邻候选集之前的相似度，通过相似度的大小去合并候选集，直到产生目标个数的候选集,

候选集的相似度计算有多种方式，有颜色、纹理、而枳和吻合相似度计算。

最后生成的L个Region Proposal与CNN相结合，这就是R-CNN名字的由来,

R-CNN作者证明了在当前任务下SVM的分类效果要比神经网络分类器好。最后每个SNM分类器都会得到图像对于该类别的得分和置信度，置信度最高的类别为改图像区域对应的预测类别

总结一下R-CNN存在的两个问题：

R-CNN在生成了候选区域后，需要对每个区域进行统一尺寸的压缩或放大，当候选集的长与宽差别较大时强行压缩至比例为1:1时会使图像产生变形和丢失图像的原始特征
R-CNN生成了多个候选集后需要全部输入到CNN中，当生成了2000个候选集时，就需要对图片进行2000次单模型特征提取，这无疑是效率低下的

针对上述的两个问题，Kaiming He等人提出了SSPNet（空间金字塔池化网络）来解决。详细了解什么是SSPNet

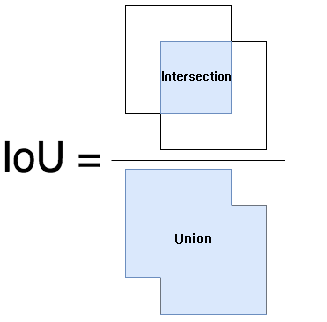
5 IoU

IoU 的全称为交并比（Intersection over Union），通过这个名称我们大概可以猜到 IoU 的计算方法。IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值。

6 卷积

卷积在图像识别中的概念是提取一幅图像的特征，通常对一幅图像进行卷积会有一个卷积核，该卷积核是一个正方形矩阵。一般是奇数矩阵，这样做的目的是为了卷积核总是有一个中心。大部分情况使用的3x3或者5x5等

详细了解什么是卷积神经网络

7 池化/下采样（pooling）

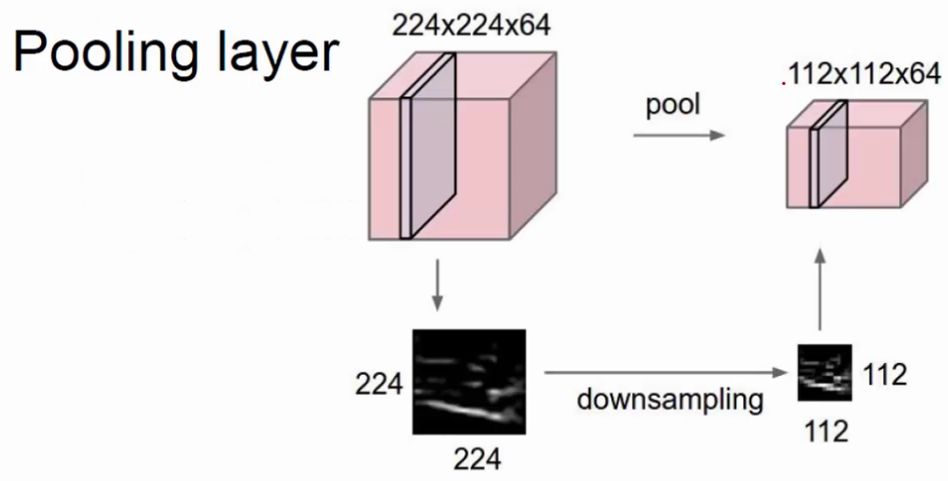
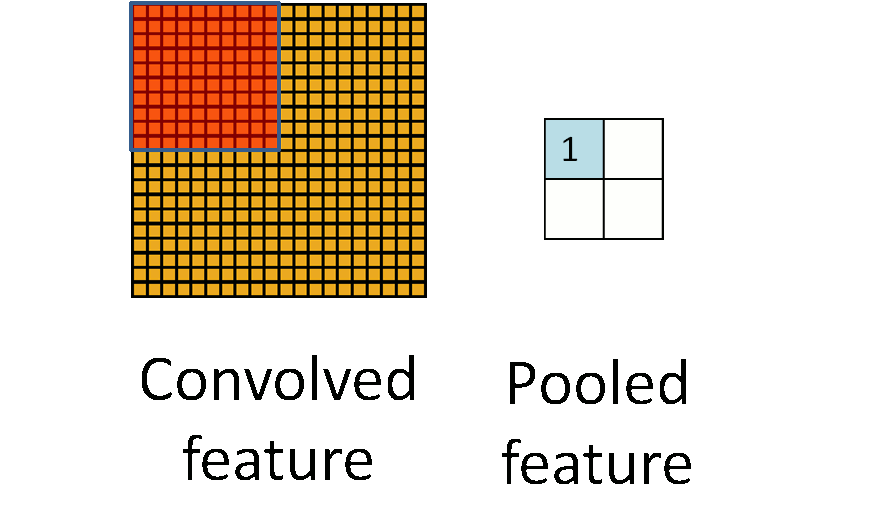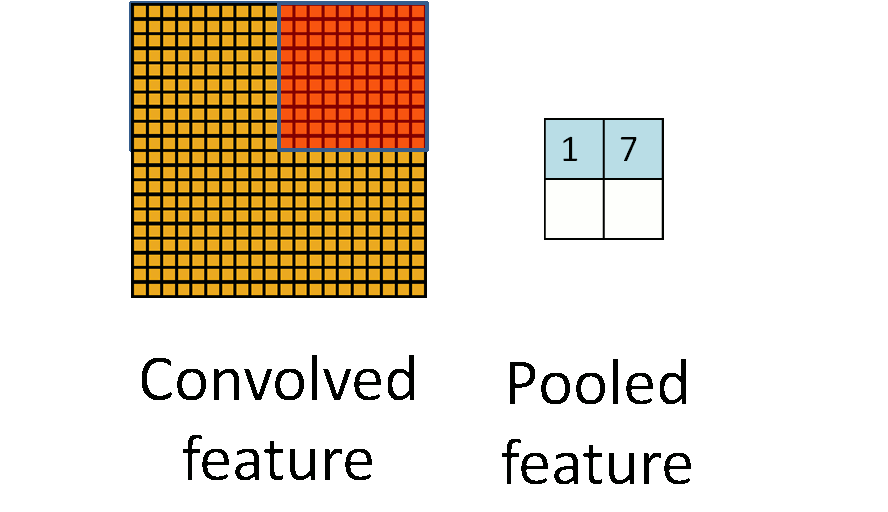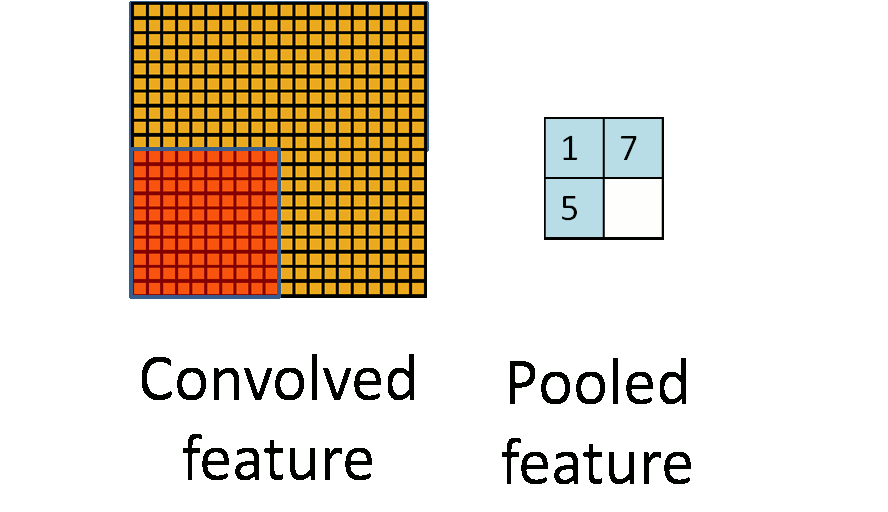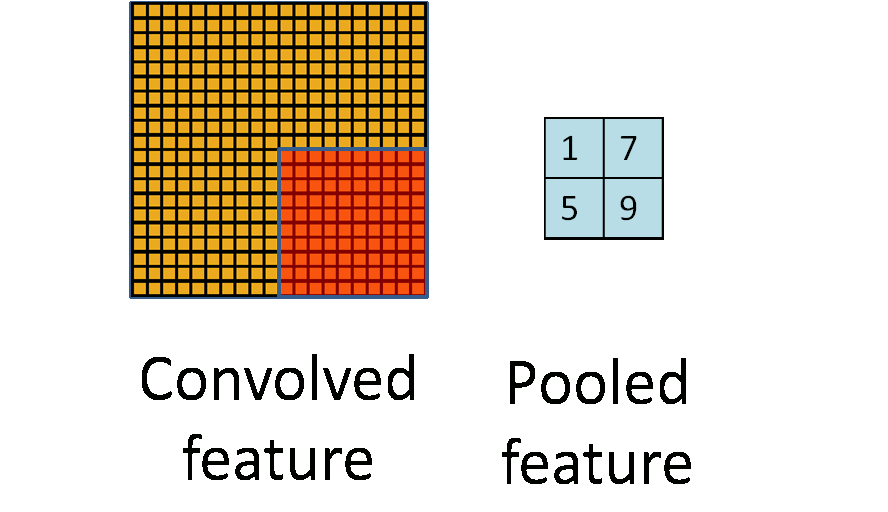
上面介绍了卷积操作，卷积的目的是提取一幅图像的特征，也就是边缘部分。但是一幅图像往往很大，有的甚至几百万的像素，每一个像素对应一个参数，那就意味着会有几百万个参数，这对于计算机的内存处理来讲是一个很大的问题。那么为了减少参数，提升计算机的运行效率，这里提出一个pooling的概念，也就是较少一部分对图像影响较小的参数，从而使得计算机的运行效率能够提升。池化操作一般在卷积之后。

如上图所示，池化就是对特征图进行特征压缩，池化也叫做下采样。选择原来某个区域的max或mean代替那个区域，整体就浓缩了

pooling有很多种，这里介绍几种：

一般池化（general pooling）
重叠池化（OverlappingPooling）
空金字塔池化（Spatial Pyramid Pooling）
还有一些池化，这篇博客有介绍

pooling layer视频介绍

7.1 General pooling

池化作用于图像中不重合的区域（这与卷积操作不同），过程如下图

我们定义池化窗口的大小为sizeX，即下图中红色正方形的边长，定义两个相邻池化窗口的水平位移/竖直位移为stride。一般池化由于每一池化窗口都是不重复的，所以sizeX=stride。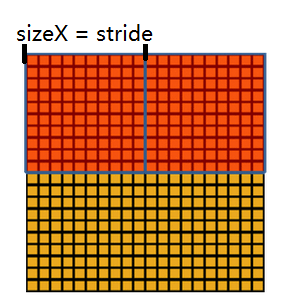

最常见的池化操作为平均池化mean pooling和最大池化max pooling：

平均池化：计算图像区域的平均值作为该区域池化后的值。

最大池化：选图像区域的最大值作为该区域池化后的值。

7.2 Overlapping pooling

重叠池化正如其名字所说的，相邻池化窗口之间会有重叠区域，此时sizeX>stride

7.3 Spatial Pyramid Pooling

空间金字塔池化可以把任何尺度的图像的卷积特征转化成相同维度，这不仅可以让CNN处理任意尺度的图像，还能避免cropping和warping操作，导致一些信息的丢失，具有非常重要的意义

一般的CNN都需要输入图像的大小是固定的，这是因为全连接层的输入需要固定输入维度，但在卷积操作是没有对图像尺度有限制，所有作者提出了空间金字塔池化，先让图像进行卷积操作，然后转化成维度相同的特征输入到全连接层，这个可以把CNN扩展到任意大小的图像。

空间金字塔池化的思想来自于Spatial Pyramid Model，它一个pooling变成了多个scale的pooling。用不同大小池化窗口作用于卷积特征，我们可以得到1X1,2X2,4X4的池化结果，由于conv5中共有256个过滤器，所以得到1个256维的特征，4个256个特征，以及16个256维的特征，然后把这21个256维特征链接起来输入全连接层，通过这种方式把不同大小的图像转化成相同维度的特征。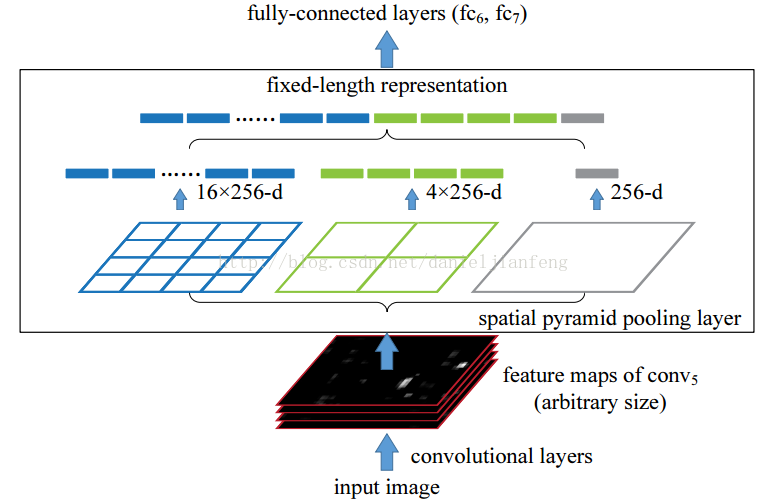

7.4 Rol pooling

Rol(Region of Interest)是图像中我们感兴趣的区域的意思，也可以理解为region proposal（候选区域）。

ROI pooling总结：
（1）用于目标检测任务；
（2）允许我们对CNN中的feature map进行reuse；
（3）可以显著加速training和testing速度；
（4）允许end-to-end的形式训练目标检测系统。

8 RPN（Region Proposal Network）

目前最先进的目标检测网络需要先用区域建议(region proposal)算法推测目标位置，像SPPnet[7]和Fast R-CNN[5]这些网络已经减少了检测网络的运行时间，这时计算区域建议(region proposal)就成了瓶颈问题。本文中，我们介绍一种区域建议网络（Region Proposal Network, RPN），它和检测网络共享全图的卷积特征(共享卷积核)，使得区域建议几乎不花时间。RPN是一个全卷积网络，在每个位置同时预测目标边界和objectness得分。RPN是端到端训练的，生成高质量区域建议框，用于Fast R-CNN来检测。通过一种简单的交替运行优化方法，RPN和Fast R-CNN可以在训练时共享卷积特征。对于非常深的VGG-16模型[19]，我们的检测系统在GPU上的帧率为5fps（包含所有步骤），在PASCAL VOC 2007和PASCAL VOC 2012上实现了最高的目标检测准确率（2007是73.2%mAP，2012是70.4%mAP），每个图像用了300个建议框。代码已公开

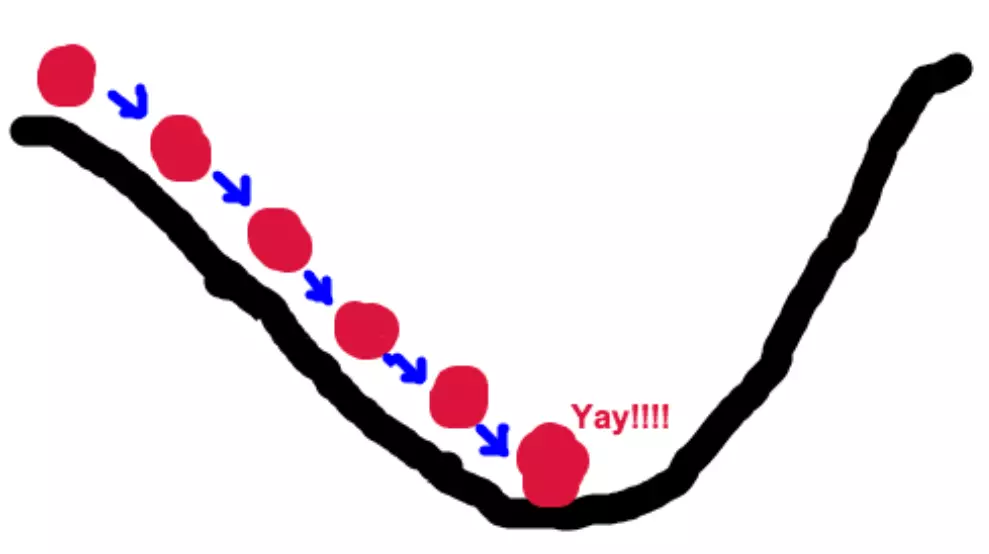
9 梯度下降

百度百科解释：梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法

详细了解什么是梯度下降

10 损失函数

损失函数（loss function）或代价函数（cost function）是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。在应用中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。

损失函数的作用：衡量模型模型预测的好坏

比如你做一个线性回归，实际值和你的预测值肯定会有误差，那么我们找到一个函数表达这个误差就是损失函数

损失函数与鲁棒性的关系：

损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。

常用的损失函数：
(1) 0-1损失函数(0-1 lossfunction):
L(Y,f(X))={1,0,Y≠f(X)Y=f(X)
(2)平方损失函数(quadraticloss function)
L(Y,f(X))=(Y−f(X))2
(3)绝对损失函数(absoluteloss function)
L(Y,f(X))=|Y−f(X)|
(4)对数损失函数(logarithmicloss function)或对数似然损失函数(log-likelihood loss function)

L(Y,P(Y|X))=−logP(Y|X)

11 激活函数

实际上．激活函数也是在模拟神经元的特点。人体的祌经元不是接收到输入就会全部输出的，是当输入达到一定的阈值后，线性或非线性的将输入转化成输出，这也就是激活函数的原理,在人工神经网络中，激活函数就在神经元的连接形式中，以非线性的映射关系而存在，是神经网络能表达复杂非线性关系的关键所在。

11.1 sigmoid函数

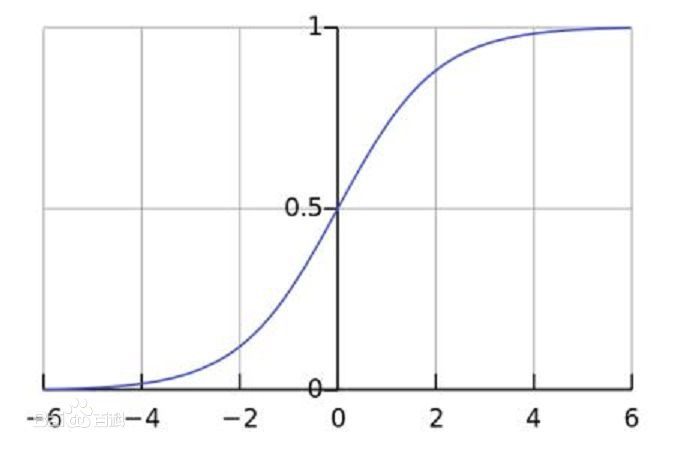
Sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。在信息科学中，由于其单增以及反函数单增等性质，Sigmoid函数常被用作神经网络的激活函数，将变量映射到0,1之间
sigmoid公式如下：

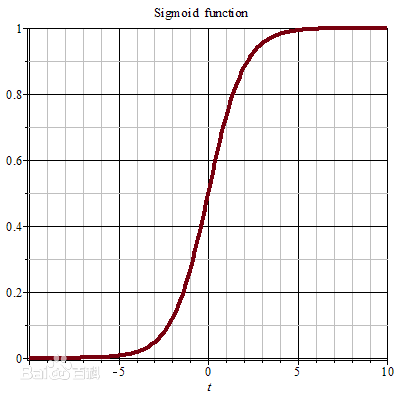
sigmoid函数图像如下：

sigmoid函数的缺点：

计算量很大
会带来梯度（函数图像中某一点的斜率，即导数）消失的问题
输入的范围基本在[-6,6]之间，当输入的数的绝对值大于6时，效果和6差不多

sigmoid函数的Python实现：

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
    return 1.0/(1+np.exp(-x))
 
sigmoid_inputs = np.arange(-10,10,0.1)
sigmoid_outputs = sigmoid(sigmoid_inputs)
print("Sigmoid Function Input :: {}".format(sigmoid_inputs))
print("Sigmoid Function Output :: {}".format(sigmoid_outputs))
 
plt.plot(sigmoid_inputs,sigmoid_outputs)
plt.xlabel("Sigmoid Inputs")
plt.ylabel("Sigmoid Outputs")
plt.show()

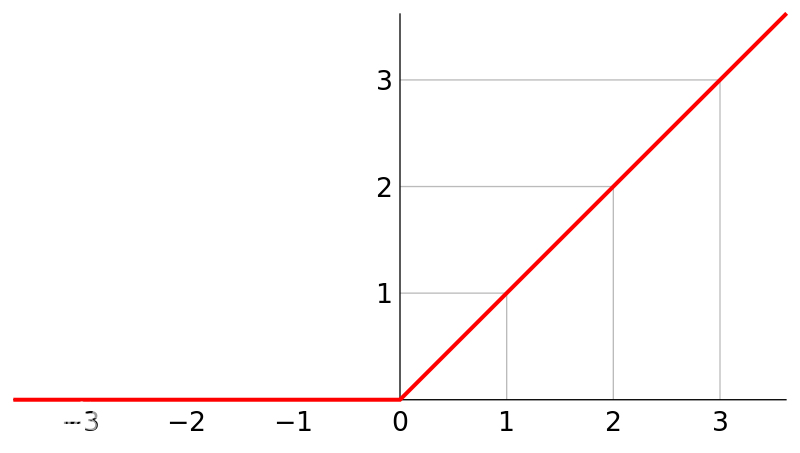
11.2 ReLU函数

ReLU函数：为了避免sigmoid函数梯度趋于０产生的梯度饱和问题，线性整流函数（Rectified Linear Unit, ReLU),被提出并在卷积神经网络中取得了不错的效果。
当输入取值小于0时ReLU不会被激活，特别是在后向传播计算中梯度很容易变为0，这是ReLU函数本身存在的硬饱和，又会带来梯度消失的问题。而且ReLU函数的输出值是不存在负数的，这代表了ReLU也不是以0为均值的函数

CNN中常用。对正数原样输出，负数直接置零。在正数不饱和，在负数硬饱和。ReLU计算上比sigmoid或者tanh更省计算量，因为不用exp，因而收敛较快。但是还是非zero-centered。
ReLU在负数区域被kill的现象叫做dead ReLU，这样的情况下，有人通过初始化的时候用一个稍微大于零的数比如0.01来初始化神经元，从而使得ReLU更偏向于激活而不是死掉，但是这个方法是否有效有争议。

ReLU的好处：

计算量很小，吗，速度很快
图像本身就没有负的像素值
解决了梯度消失的问题

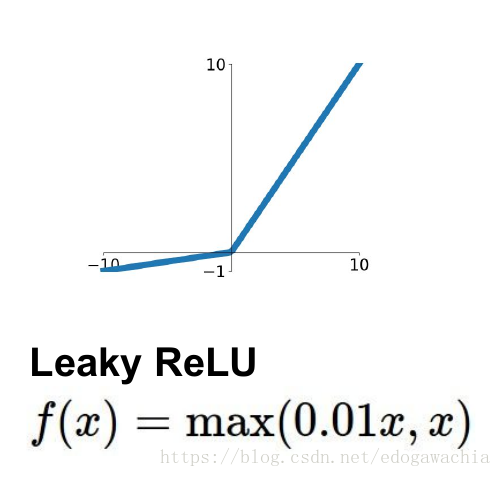
11.3 LeakyReLU函数

为了解决上述的dead ReLU现象。这里选择一个数，让负数区域不在饱和死掉。这里的斜率都是确定的。

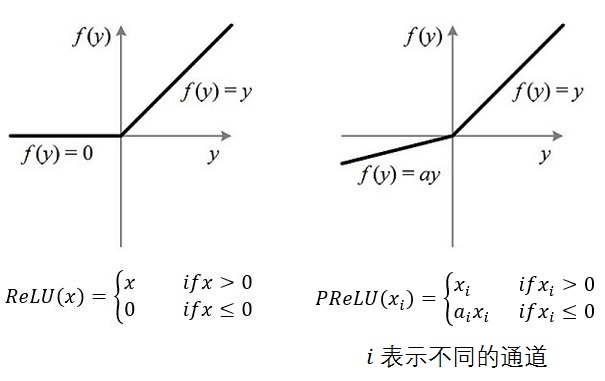
11.4 PReLU函数

PReLU(Parametric Rectified Linear Unit)顾名思义：带参数的ReLU,PReLU函数是为了解决ReLU的硬饱和问题产生的激活函数，在LeakyReLU函数中，斜率是固定的，这里的PRelu函数的斜率a是不固定的一个值，这个值可以在运算过程中不算学习改变原来的值。计算量不是很大，因为不用计算exp

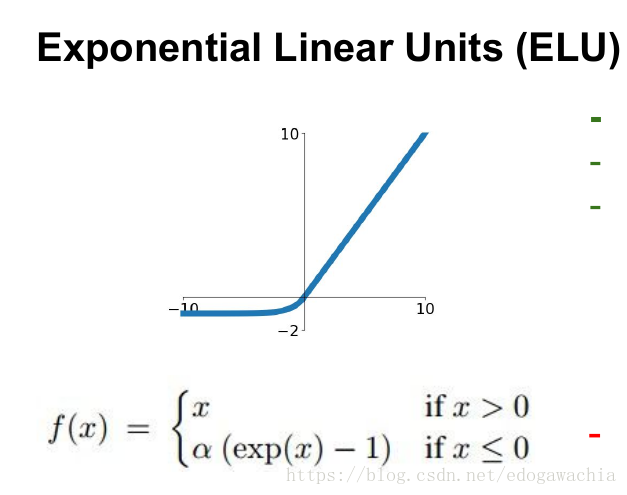
11.5 ELU函数

ELU函数是Sigmoid函数和ReLU函数的结合体，它的提出主要是为了解决ReLUＵ函数输入负值时陷入卡死的问题
具有ReLU的优势，且输出均值接近零，实际上PReLU和LeakyReLU都有这一优点。有负数饱和区域，从而对噪声有一些鲁棒性。可以看做是介于ReLU和LeakyReLU之间的一个东西。当然，这个函数也需要计算exp，从而计算量上更大一些。
ELU的优点：
和PReLU一样，ELU也引入了可学习的斜率a，使得激活函数在负半段是存在输出值的。但是和PReLU不一样的是，当输入值小于０时ELU的结构为非线性单元，这使得ELU具有良好的鲁棒性和抗干扰能力，但是还是具有一定程度的软饱和性

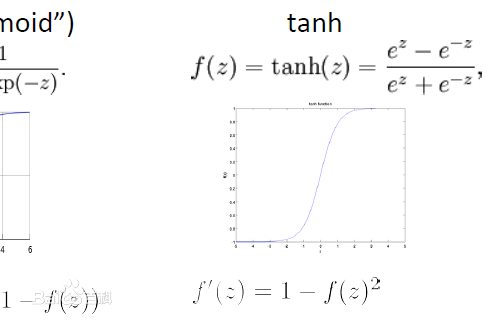
11.6 tan(h)函数

tanh是双曲函数中的一个，tanh()为双曲正切。在数学中，双曲正切“tanh”是由双曲正弦和双曲余弦这两种基本双曲函数推导而来。
tan(h)函数的公式为：

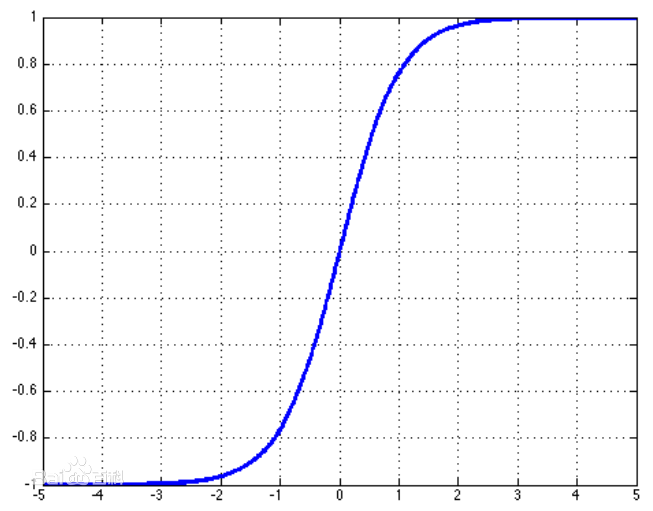
tan(h)函数的图像为：

11.7 softmax函数

softmax逻辑回归模型是logistic回归模型在多分类问题上的推广，在多分类问题中，类标签y可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的，该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的，不过后面也会介绍它与深度学习无监督学习方法的结合。

公式：

12 残差（Residual）

残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话，我们可以将残差看作误差的观测值。

比如：
y_true=10,y^=9.8,residual=y_true-y^=0.2

13 残差(Residual)和损失(loss)函数的区别

什么是残差：

残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话，我们可以将残差看作误差的观测值。

比如：
y_true=10,y^=9.8,re

sidual=y_true-y^=0.2

什么是损失：

损失函数（loss function）或代价函数（cost function）是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。在应用中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。

14 生成对抗网络（GAN）

生成式对抗网络（GAN, Generative Adversarial Networks ）是一种深度学习模型，是近年来复杂分布上无监督学习最具前景的方法之一。模型通过框架中（至少）两个模块：生成模型（Generative Model）和判别模型（Discriminative Model）的互相博弈学习产生相当好的输出。原始 GAN 理论中，并不要求 G 和 D 都是神经网络，只需要是能拟合相应生成和判别的函数即可。但实用中一般均使用深度神经网络作为 G 和 D 。一个优秀的GAN应用需要有良好的训练方法，否则可能由于神经网络模型的自由性而导致输出不理想。

详细了解生成对抗网络