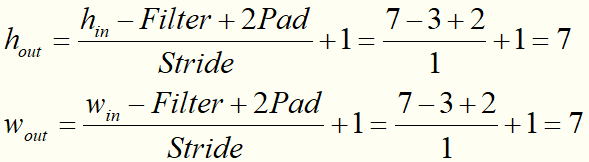关于卷积神经网络，了解一下

1 卷积神经网络

一篇很好的关于理解卷积神经网络的博客（博客中的filter助手表示的是卷积核的意思）
一篇关于如何搭建CNN的博客
 知乎回答：能否对卷积神经网络工作原理做一个直观的解释？
机器视角：长文揭秘图像处理和卷积神经网络架构|该文原文
定义：卷积神经网络（Convolutional Neural Network，CNN）是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。它包括卷积层(convolutional layer)和池化层(pooling layer)

1.1 卷积神经网络的结构：

卷积神经网络的结构包括：

输入层（input，输入一张全尺寸的黑白或彩色图像）
卷积层（filter，对ROI(region of interest)进行特征提取，一个CNN可以有很多的卷积核也可以有很多的卷积层）
池化层（pooling，可选，目的是减少上层的输入参数）
输出层（也叫全连接层FC，该层可以用来对图像进行分类和识别操作）

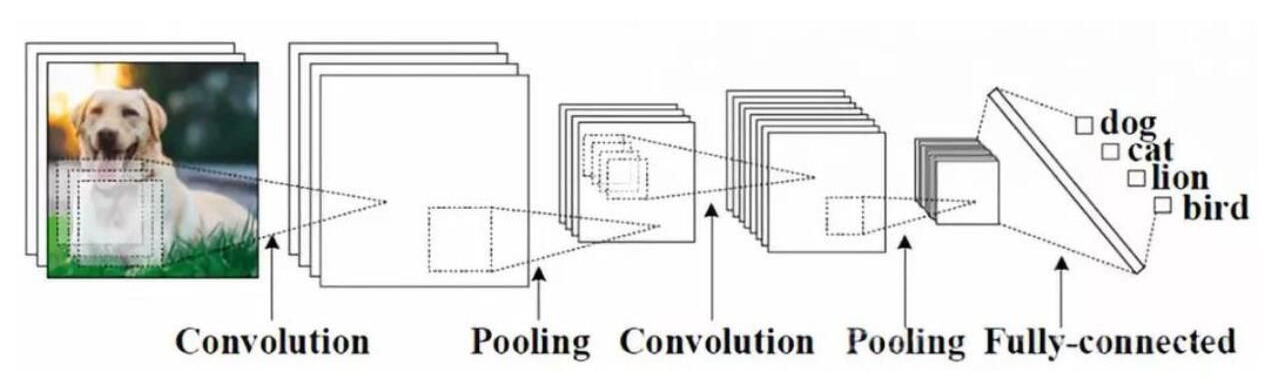
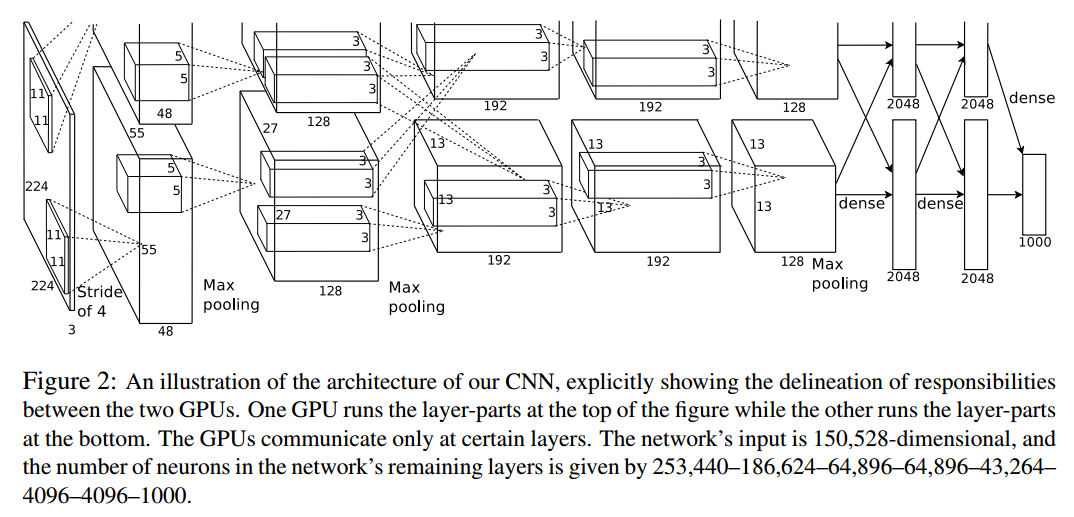
下面这张图是CNN的结构图：

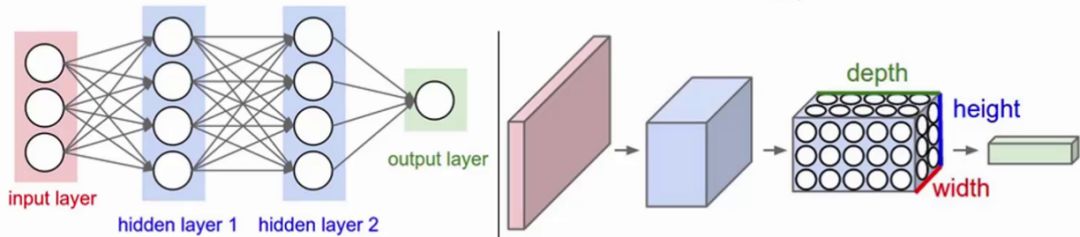
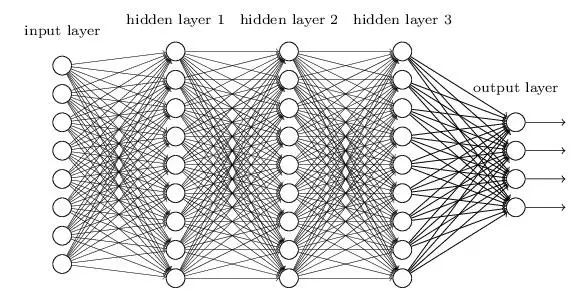
人工神经网络和卷积神经网络的对比：

左图：全连接神经网络（平面），组成：输入层、激活函数、全连接层
右图：卷积神经网络（立体），组成：输入层、卷积层、激活函数、池化层、全连接层
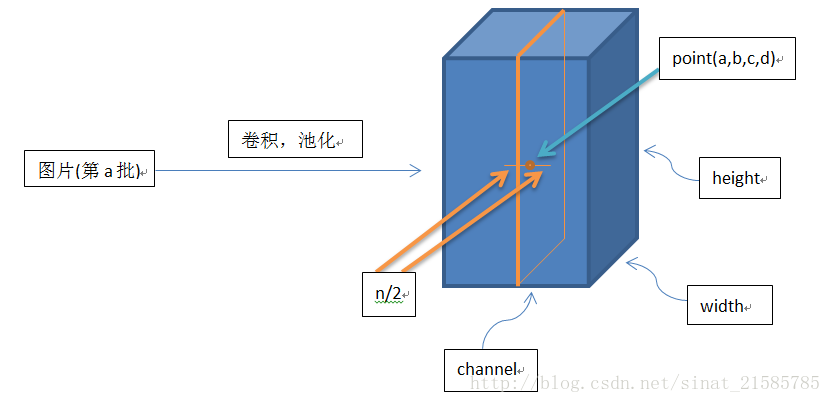
在卷积神经网络中有一个重要的概念：深度，它是指一幅图像的通道数量，如：RGB图像的深度是3，灰度图像的深度是1等
在卷积神经网络中，有一个非常重要的特性：权值共享： 所谓的权值共享就是说，给一张输入图片，用一个filter去扫这张图，filter里面的数就叫权重，这张图每个位置是被同样的filter扫的，所以权重是一样的，也就是共享。

注意：特征提取之后，一般使用几个filter助手（卷积核）就会得到几个深度为1的feature map

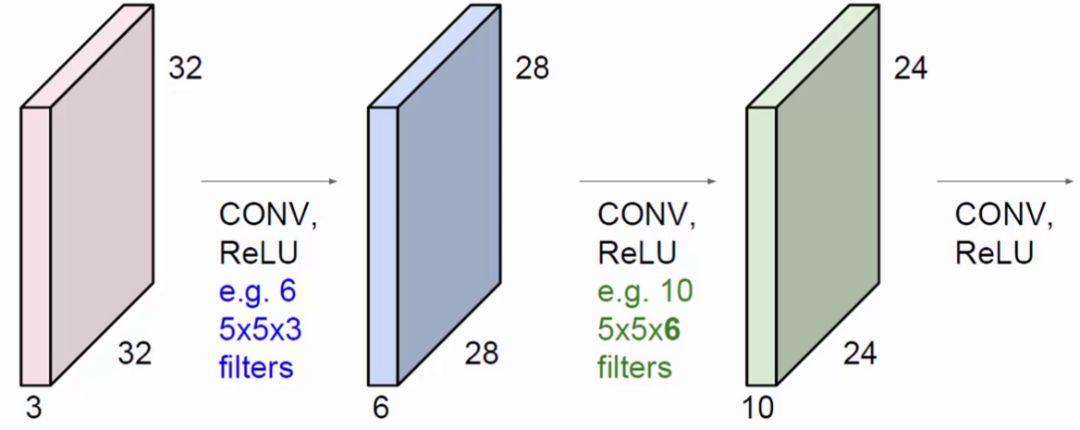
卷积不仅限于对原始输入的卷积。蓝色方块是在原始输入上进行卷积操作，使用了6个filter得到了6个提取特征图。绿色方块还能对蓝色方块进行卷积操作，使用了10个filter得到了10个特征图。每一个filter的深度必须与上一层输入的深度相等。

更加直观理解卷积：

以上图为例：
第一次卷积可以提取出低层次的特征。
第二次卷积可以提取出中层次的特征。
第三次卷积可以提取出高层次的特征。
特征是不断进行提取和压缩的，最终能得到比较高层次特征，简言之就是对原式特征一步又一步的浓缩，最终得到的特征更可靠。利用最后一层特征可以做各种任务：比如分类、回归等。

1.2 卷积的计算流程：

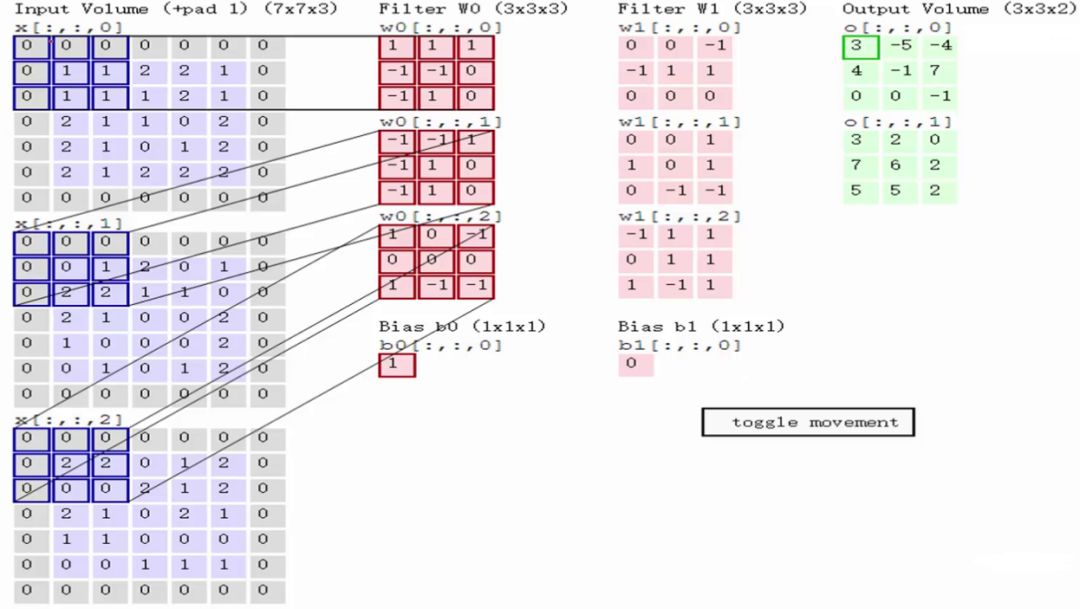
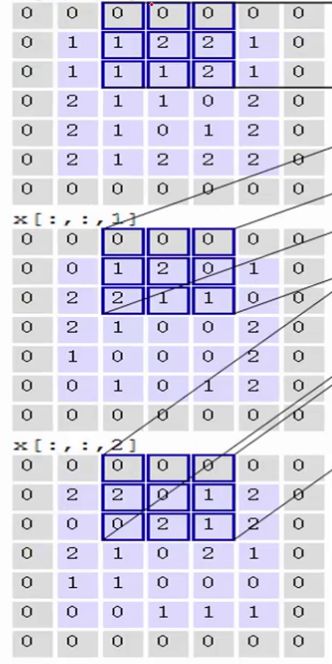
左区域的三个大矩阵是原式图像的输入，RGB三个通道用三个矩阵表示，大小为7x7x3。
Filter W0表示1个filter助手，尺寸为3*3，深度为3（三个矩阵）；Filter W1也表示1个filter助手。因为卷积中我们用了2个filter，因此该卷积层结果的输出深度为2（绿色矩阵有2个）。
Bias b0是Filter W0的偏置项，Bias b1是Filter W1的偏置项。
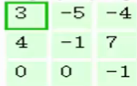
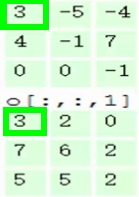
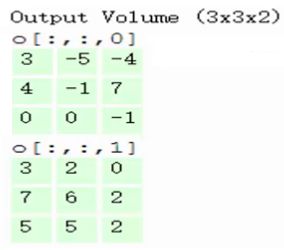
OutPut是卷积后的输出，尺寸为3x3，深度为2。

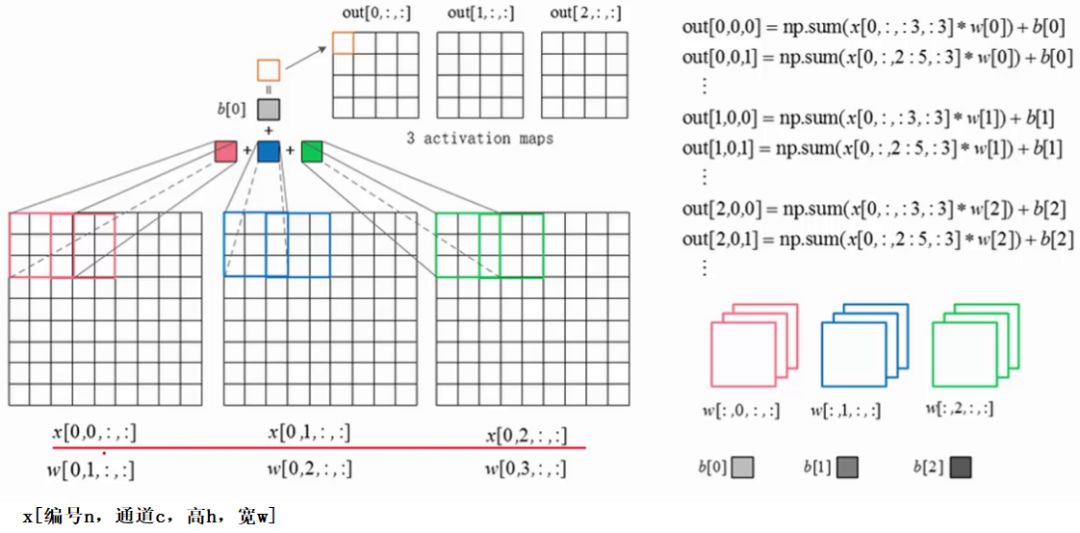
计算过程：

输入是固定的，filter是指定的，因此计算就是如何得到绿色矩阵。
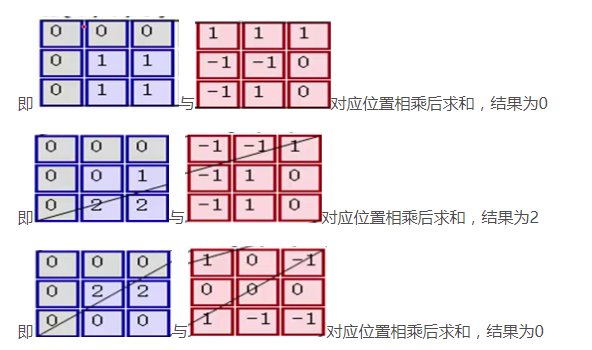
第一步，在输入矩阵上有一个和filter相同尺寸的滑窗，然后输入矩阵的在滑窗里的部分与filter矩阵对应位置相乘：

第二步，将3个矩阵产生的结果求和，并加上偏置项，即0+2+0+1=3，因此就得到了输出矩阵的左上角的3：

第三步，让每一个filter都执行这样的操作，便可得到第一个元素：

第四步，滑动窗口2个步长，重复之前步骤进行计算

第五步，最终可以得到，在2个filter下，卷积后生成的深度为2的输出结果：

思考：

为什么每次滑动是2个格子？

滑动的步长叫stride记为S。S越小，提取的特征越多，但是S一般不取1，主要考虑时间效率的问题。S也不能太大，否则会漏掉图像上的信息。

由于filter的边长大于S，会造成每次移动滑窗后有交集部分，交集部分意味着多次提取特征，尤其表现在图像的中间区域提取次数较多，边缘部分提取次数较少，怎么办？

一般方法是在图像外围加一圈0，细心的同学可能已经注意到了，在演示案例中已经加上这一圈0了，即+pad 1。 +pad n表示加n圈0.

一次卷积后的输出特征图的尺寸是多少呢？

==注意：在一层卷积操作里可以有多个filter，他们是尺寸必须相同。==

1.3 卷积神经网络的组成：

卷积——激活——卷积——激活——池化——……——池化——全连接——分类或回归

1.4 前向传播与反向传播

1.4.1 前向传播

1.4.2 反向传播

1.4.3 训练一个CGGNet需要的内存开销

1.2 残差网络(Residual Network)

论文出处：Deep Residual Learning for Image Recognition.pdf

残差网络是由来自Microsoft Research的4位学者提出的卷积神经网络，在2015年的ImageNet大规模视觉识别竞赛（ImageNet Large Scale Visual Recognition Challenge, ILSVRC）中获得了图像分类和物体识别的优胜。残差网络的特点是容易优化，并且能够通过增加相当的深度来提高准确率。其内部的残差块使用了跳跃连接，缓解了在深度神经网络中增加深度带来的梯度消失问题

我们都知道增加网络的宽度和深度可以很好的提高网络的性能，深的网络一般都比浅的的网络效果好，比如说一个深的网络A和一个浅的网络B，那A的性能至少都能跟B一样，为什么呢？因为就算我们把B的网络参数全部迁移到A的前面几层，而A后面的层只是做一个等价的映射，就达到了B网络的一样的效果。一个比较好的例子就是VGG，该网络就是在AlexNex的基础上通过增加网络深度大幅度提高了网络性能。
对于原来的网络，如果简单地增加深度，会导致梯度弥散或梯度爆炸。对于该问题的解决方法是正则化初始化和中间的正则化层（Batch Normalization），这样的话可以训练几十层的网络。
虽然通过上述方法能够训练了，但是又会出现另一个问题，就是退化问题，网络层数增加，但是在训练集上的准确率却饱和甚至下降了。这个不能解释为overfitting，因为overfit应该表现为在训练集上表现更好才对。退化问题说明了深度网络不能很简单地被很好地优化。作者通过实验：通过浅层网络等同映射构造深层模型，结果深层模型并没有比浅层网络有等同或更低的错误率，推断退化问题可能是因为深层的网络并不是那么好训练，也就是求解器很难去利用多层网络拟合同等函数。

1.3 梯度消失

概念
在神经网络中，当前面隐藏层的学习速率低于后面隐藏层的学习速率，即随着隐藏层数目的增加，分类准确率反而下降了。这种现象叫做消失的梯度问题
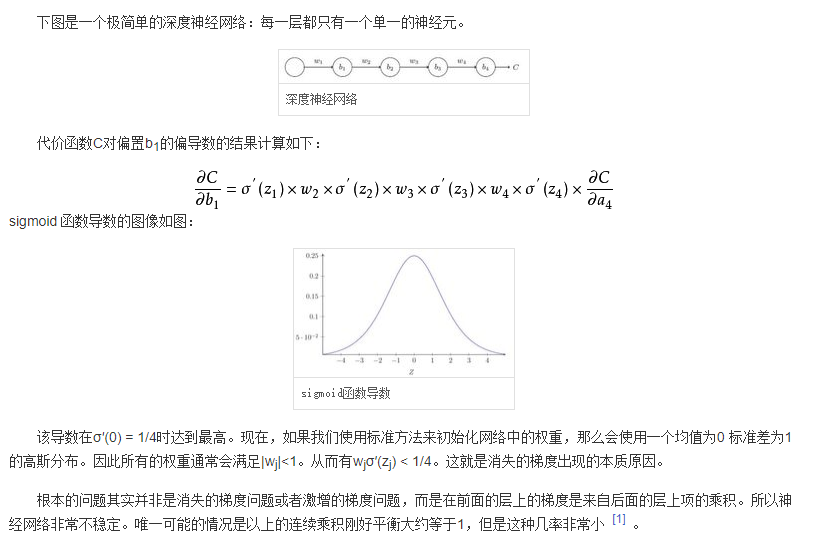
梯度消失产生的原因

1.4 梯度爆炸

梯度爆炸是梯度消失（梯度弥散）的对立面

1.5 梯度消失和梯度爆炸的解决方案

举个例子，对于一个含有三层隐藏层的简单神经网络来说，当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习。

==梯度消失和梯度爆炸本质上是一样的，都是因为网络层数太深而引发的梯度反向传播中的连乘效应。==
解决方案：

换用Relu、LeakyRelu、Elu等激活函数
ResNet残差结构
BatchNormalization BN本质上是解决传播过程中的梯度问题
LSTM结构 LSTM不太容易发生梯度消失，主要原因在于LSTM内部复杂的“门（gates）”，具体看LSTM基本原理解析
预训练加finetunning 此方法来自Hinton在06年发表的论文上，其基本思想是每次训练一层隐藏层节点，将上一层隐藏层的输出作为输入，而本层的输出作为下一层的输入，这就是逐层预训练。训练完成后，再对整个网络进行“微调（fine-tunning）”。此方法相当于是找全局最优，然后整合起来寻找全局最优，但是现在基本都是直接拿imagenet的预训练模型直接进行finetunning。
梯度剪切、正则
这个方案主要是针对梯度爆炸提出的，其思想是设值一个剪切阈值，如果更新梯度时，梯度超过了这个阈值，那么就将其强制限制在这个范围之内。这样可以防止梯度爆炸。
另一种防止梯度爆炸的手段是采用权重正则化，正则化主要是通过对网络权重做正则来限制过拟合，但是根据正则项在损失函数中的形式可以看出，如果发生梯度爆炸，那么权值的范数就会变的非常大，反过来，通过限制正则化项的大小，也可以在一定程度上限制梯度爆炸的发生。