一篇文看透二叉树，先序遍历、中序遍历、后序遍历、广度优先、深度优先，java实现

1 二叉树的定义

在计算机科学中，二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

二叉树的第$i$层至多拥有$2^{i-1}$个节点；深度为$k$的二叉树至多总共有$2^k-1$个节点（定义根节点所在深度$k_0=0$)，而总计拥有节点数符合的，称为“满二叉树”；深度为$k$有$n$个节点的二叉树，当且仅当其中的每一节点，都可以和同样深度的满二叉树，序号为1到$n$的节点一对一对应时，称为完全二叉树。对任何一棵非空的二叉树$T$，如果其叶片（终端节点）数为$n_0$，分支度为2的节点数为$n_2$，则$n_0=n_2+1$。

与普通树不同，普通树的节点个数至少为1，而二叉树的节点个数可以为0；普通树节点的最大分支度没有限制，而二叉树节点的最大分支度为2；普通树的节点无左、右次序之分，而二叉树的节点有左、右次序之分。

二叉树通常作为数据结构应用，典型用法是对节点定义一个标记函数，将一些值与每个节点相关系。这样标记的二叉树就可以实现二叉搜索树和二叉堆，并应用于高效率的搜索和排序。

2 完全二叉树和满二叉树

	完全二叉树	满二叉树
总节点k	$2^{h-1}<=k<=2^h-1$	$k=2^h-1$
树高h	$h=log_2k+1$	$h=log_2{(k+1)}$

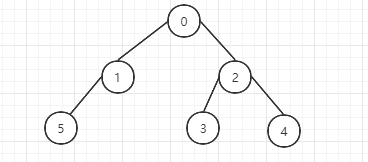
3 二叉树的遍历

3.1 先序遍历

先序遍历的顺序是：先根节点，再左节点，再右节点，即根节点->左节点->右节点。

如：

先序遍历的顺序为：0,1,5,2,3,4

• 采用递归实现

public void beforeOrder(MyTreeNode root) {
    if (root != null) {
        System.out.println(root.data);
        beforeOrder(root.leftChild);
        beforeOrder(root.rightChild);
    }
}

• 非递归实现

  实现栈这种数据结构，存储还没有遍历的节点，由于顺序是根->左->右，所以先将右节点压入栈中，这样就可以实现先访问左边的节点的目的了。

public void preOrder(MyTreeNode root){
    QueueToStack<MyTreeNode> stack = new QueueToStack<>();
    stack.push(root);
    MyTreeNode node;
    while (!stack.empty()){
        node = stack.pop();
        System.out.println(node.data);
        if (node.rightChild!=null){
            stack.push(node.rightChild);
        }
        if (node.leftChild!=null){
            stack.push(node.leftChild);
        }
    }
}

3.2 中序遍历

中序遍历的顺序为，先左节点，再根节点，再右节点，即左节点->根节点->右节点。

还是以下面的二叉树为例：

中序遍历的顺序为：5,1,0,3,2,4

• 递归实现

public void middleOrder(MyTreeNode root) {
    if (root != null) {
        middleOrder(root.leftChild);
        System.out.println(root.data);
        middleOrder(root.rightChild);
    }
}

• 非递归实现

  由于中序遍历的顺序是：左->根->右，所有先将所有左节点压入栈中，如果遇到最后一个叶子节点没有左节点了，那么就将当前节点的数据输出，此时继续遍历当前节点的右节点。第12行代码，为什么不需要判断右节点是否为空，因为如果右节点为空的话，那么就不要继续遍历了，前面的while循环会判断是否为空。

public void inOrder(MyTreeNode root) {
    QueueToStack<MyTreeNode> stack = new QueueToStack<>();
    MyTreeNode node = root;
    while (node != null || !stack.empty()) {
        while (node != null) {
            stack.push(node);
            node = node.leftChild;
        }
        if (!stack.empty()) {
            node = stack.pop(); //叶子节点的父节点
            System.out.println(node.data);
            node = node.rightChild; //父节点的右节点，可能为null
        }
    }
}

3.3 后序遍历

后序遍历的顺序是：先左节点，再右节点，再根节点，即左节点->右节点->根节点。

还是以上面的二叉树为例：

后序遍历的顺序为：5,1,3,4,2,0

• 递归实现

public void behindOrder(MyTreeNode root) {
    if (root != null) {
        behindOrder(root.leftChild);
        behindOrder(root.rightChild);
        System.out.println(root.data);
    }
}

• 非递归实现1

  后续遍历的非递归实现是这三种方式中最难实现的一种，因为根节点是最后才被访问的，所以需要对之前的节点进行记忆。即将上一次访问过的节点记录下来，当遇到没有左、右子节点的叶子节点时，先判断当前叶子节点的父节点的右子节点是否被访问过，如果没有被访问过，则继续遍历右节点（这个右节点是叶子节点的兄弟节点）；如果被访问过，则打印当前的叶子节点。

public void afterOrder(MyTreeNode root) {
    QueueToStack<MyTreeNode> stack = new QueueToStack<>();
    MyTreeNode node = root;
    MyTreeNode lastVisit = root;//记录上一次遍历过的节点
    while (!stack.empty() || node != null) {
        while (node != null) {
            stack.push(node);
            node = node.leftChild;
        }
        node = stack.top();
        if (node.rightChild==null||node.rightChild==lastVisit){
            System.out.println(node.data);
            stack.pop();
            lastVisit = node;
            node=null;
        }else{
            node = node.rightChild;
        }
    }
}

• 非递归实现2

  我们知道，二叉树的前中后的遍历依次为以下顺序：

  • 前序遍历：root->left->right。
  • 中序遍历：left->root->right
  • 后序遍历：left->right->root

  我们发现后序遍历和前序遍历有些地方比较相似，我们可以借鉴前序遍历的非递归实现，从而快速实现后续遍历的非递归实现。我们发现后续遍历相当于是前序遍历的一个反序，只不过反过来之后将左右孩子的遍历顺序交换了一下，但是没有关系，我们先来回顾一下前序遍历的非递归实现代码：

  public List<Integer> preorderTraversal(TreeNode root) {
      List<Integer> res = new ArrayList<>();
      if (root == null) return res;
      Deque<TreeNode> stk = new ArrayDeque<>();
      stk.addLast(root);
      while (!stk.isEmpty()) {
          TreeNode t = stk.pollLast();
          res.add(t.val);
          if (t.right != null) stk.addLast(t.right);
          if (t.left != null) stk.addLast(t.left);
      }
      return res;
  }

  从代码中可以看待，因为栈是一种先进后出的数据结构，所以如果前序遍历想要先访问左子树，那么就需要先将右子树压入栈中。同理，在后序遍历中，我们将后序遍历的顺序反序遍历，将left->right->root的遍历顺序改成root->right->left。那么在添加到结果集的时候，也需要对其添加顺序进行反序，所以就有了下面的代码：

  public List<Integer> postorderTraversal(TreeNode root) {
      List<Integer> res = new ArrayList<>();
      if (root == null) return res;
      Deque<TreeNode> stk = new ArrayDeque<>();
      stk.addLast(root);
      while (!stk.isEmpty()) {
          TreeNode t = stk.pollLast();
          res.add(0, t.val); //每次将结果添加到结果集的最前面
          if (t.left != null) stk.addLast(t.left); //这里和前序遍历的操作刚好相反
          if (t.right != null) stk.addLast(t.right);
      }
      return res;
  }

3.4 广度优先遍历

广度优先遍历的顺序是：从根节点向下，从左到右遍历，下面还是拿上面的二叉树为例：

广度优先遍历顺序为：0,1,2,5,3,4

• 使用队列进行遍历的java实现

public void breadthOrder(MyTreeNode root) throws InterruptedException {
    StackToQueue<MyTreeNode> queue = new StackToQueue();//这是我自己写的一个队列，可以使用java自带的队列
    queue.push(root);
    while (queue.size() > 0) {
        root = queue.pop();
        System.out.println(root.data);
        if (root.leftChild != null)
            queue.push(root.leftChild);
        if (root.rightChild != null)
            queue.push(root.rightChild);
    }
}

3.5 深度优先遍历

深度优先遍历的顺序为：先从根节点一直往下直到叶子节点进行遍历，然后叶子节点回到其父节点的右节点进行遍历。

深度优先遍历顺序：0,1,5,2,3,4

• 使用栈进行遍历的java实现

public void deepthOrder(MyTreeNode root) {
        QueueToStack<MyTreeNode> stack = new QueueToStack();
        stack.push(root);
        while (!stack.empty()) {
            root = stack.pop();
            System.out.println(root.data);
            if (root.rightChild != null)
                stack.push(root.rightChild);
            if (root.leftChild != null)
                stack.push(root.leftChild);

        }
    }

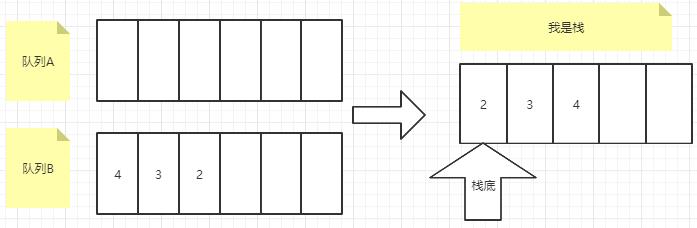
4 二叉树的实现

4.1 QueueToStack.java

package tree;

import java.util.LinkedList;
import java.util.Queue;

public class QueueToStack<T> {
    Queue<T> queueA = new LinkedList<>();
    Queue<T> queueB = new LinkedList<>();

    /**
     * Push element x onto stack.
     */
    public void push(T x) {
        if (queueA.isEmpty() && !queueB.isEmpty()) {
            queueA.add(x);
            while (!queueB.isEmpty()){
                T data = queueB.remove();
                queueA.add(data);
            }

        } else if (!queueA.isEmpty() && queueB.isEmpty()) {
            queueB.add(x);
            while (!queueA.isEmpty()){
                T data = queueA.remove();
                queueB.add(data);
            }

        } else if (queueA.isEmpty() && queueB.isEmpty()) {
            queueA.add(x);
        }
    }

    /**
     * Removes the element on top of the stack and returns that element.
     */
    public T pop() {
        if (queueA.isEmpty() && !queueB.isEmpty())
            return queueB.remove();
        return queueA.remove();

    }

    /**
     * Get the top element.
     */
    public T top() {
        if (queueA.isEmpty() && !queueB.isEmpty())
            return queueB.peek();
        return queueA.peek();
    }

    /**
     * Returns whether the stack is empty.
     */
    public boolean empty() {
        if (queueA.isEmpty() && queueB.isEmpty())
            return true;
        return false;
    }
}

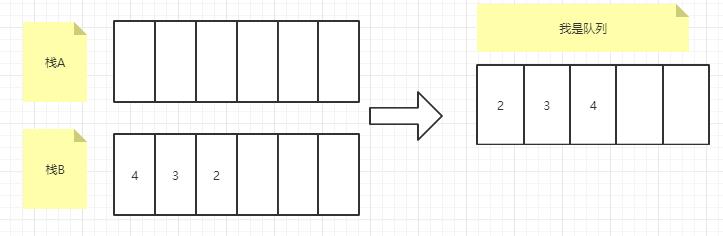
4.2 StackToQueue.java

package tree;

import java.util.Stack;

/*
用两个栈实现队列的功能
 */
public class StackToQueue<T> {

    Stack<T> stackA = new Stack<>();
    Stack<T> stackB = new Stack<>();

    //push a data to the stack
    public void push2(T data) {
        if (stackA.empty() && !stackB.empty()) {
            while (!stackB.empty()) {
                stackA.push(stackB.pop());
            }
        }
        //A is not empty, so push the data to A
        stackA.push(data);
    }

    //remove the top element data
    public T pop2() {
        if (stackA.empty() && stackB.empty())//都为空时
//            System.out.println("null");
            return null;
        else if (!stackA.empty()) {//执行pop之前的操作，都是push，此时栈B是空的
            while (!stackA.empty())
                stackB.push(stackA.pop());
            return stackB.pop();
        } else// if (stackA.empty() && !stackB.empty())//上一步执行的pop操作，栈A是空的，
            return stackB.pop();
    }

    //print the top element data
    public T peek2() {
        if (stackA.empty() && stackB.empty())//都为空时
//            System.out.println("null");
            return null;
        else if (!stackA.empty()) {//执行pop之前的操作，都是push，此时栈B是空的
            while (!stackA.empty())
                stackB.push(stackA.pop());
            return stackB.peek();
//            System.out.println(stackB.peek());
        } else //if (stackA.empty() && !stackB.empty())//上一步执行的pop操作，栈A是空的，
//            System.out.println(stackB.peek());
            return stackB.peek();

    }

    public void push(T x) {
        if (stackA.empty()) {
            stackA.push(x);
        } else {
            while (!stackA.empty())
                stackB.push(stackA.pop());
            stackA.push(x);
            while (!stackB.empty())
                stackA.push(stackB.pop());
        }
    }

    public T pop() {
        if (!stackA.empty())
            return stackA.pop();
        return null;
    }

    public void peek() {
        if (!stackA.empty())
            System.out.println(stackA.peek());
    }

    public int size() {
        return stackA.size();
//        System.out.println(stackA.size());
    }
}

4.3 MyTreeNode.java

package tree;

public class MyTreeNode<T> {
    T data;
    MyTreeNode leftChild;
    MyTreeNode rightChild;

    public void addLeftChild(T data) {
        if (data != null)
            this.leftChild = new MyTreeNode(data);
    }

    public void addRightChild(T data) {
        if (data != null)
            this.rightChild = new MyTreeNode(data);
    }

    public MyTreeNode(T data) {
        this.data = data;
    }

    public MyTreeNode() {
        this.data = null;
        this.leftChild = null;
        this.rightChild = null;
    }

    public MyTreeNode(T data, MyTreeNode leftChild, MyTreeNode rightChild) {
        this.data = data;
        this.leftChild = leftChild;
        this.rightChild = rightChild;
    }

    public boolean isLeaf() {
        if (this.leftChild == null && this.rightChild == null) {
            return true;
        }
        return false;
    }

    //递归实现
    //前序遍历，先打印根节点数据，在遍历左节点，在遍历右节点
    public void beforeOrder(MyTreeNode root) {
        if (root != null) {
            System.out.println(root.data);
            beforeOrder(root.leftChild);
            beforeOrder(root.rightChild);
        }
    }

    //非递归的先序遍历 root -> left -> right
    public void preOrder(MyTreeNode root) {
        QueueToStack<MyTreeNode> stack = new QueueToStack<>();
        stack.push(root);
        MyTreeNode node;
        while (!stack.empty()) {
            node = stack.pop();
            System.out.println(node.data);
            while (node.rightChild != null) {
                stack.push(node.rightChild);
            }
            while (node.leftChild != null) {
                stack.push(node.leftChild);
            }
        }
    }

    //中序遍历，先遍历左节点，然后遍历根节点，再遍历右节点
    public void middleOrder(MyTreeNode root) {
        if (root != null) {
            middleOrder(root.leftChild);
            System.out.println(root.data);
            middleOrder(root.rightChild);
        }
    }

    //非递归的中序遍历 left -> root -> right
    public void inOrder(MyTreeNode root) {
        QueueToStack<MyTreeNode> stack = new QueueToStack<>();
        MyTreeNode node = root;
        while (node != null || !stack.empty()) {
            while (node != null) {
                stack.push(node);
                node = node.leftChild;
            }
            if (!stack.empty()) {
                node = stack.pop(); //叶子节点的父节点
                System.out.println(node.data);
                node = node.rightChild; //父节点的右节点，可能为null
            }
        }
    }

    //中序遍历，先遍历左节点，然后遍历根节点，再遍历右节点
    public void behindOrder(MyTreeNode root) {
        if (root != null) {
            behindOrder(root.leftChild);
            behindOrder(root.rightChild);
            System.out.println(root.data);
        }
    }

    //非递归的后序遍历
    public void afterOrder(MyTreeNode root) {
        QueueToStack<MyTreeNode> stack = new QueueToStack<>();
        MyTreeNode node = root;
        MyTreeNode lastVisit = root;//记录上一次遍历过的节点
        while (!stack.empty() || node != null) {
            while (node != null) {
                stack.push(node);
                node = node.leftChild;
            }
            node = stack.top();
            if (node.rightChild==null||node.rightChild==lastVisit){
                System.out.println(node.data);
                stack.pop();
                lastVisit = node;
                node=null;
            }else{
                node = node.rightChild;
            }
        }
    }

    public void breadthOrder(MyTreeNode root) throws InterruptedException {
        StackToQueue<MyTreeNode> queue = new StackToQueue();
        queue.push(root);
        while (queue.size() > 0) {
            root = queue.pop();
            System.out.println(root.data);
            if (root.leftChild != null)
                queue.push(root.leftChild);
            if (root.rightChild != null)
                queue.push(root.rightChild);
        }
    }

    public void deepthOrder(MyTreeNode root) {
        QueueToStack<MyTreeNode> stack = new QueueToStack();
        stack.push(root);
        while (!stack.empty()) {
            root = stack.pop();
            System.out.println(root.data);
            if (root.rightChild != null)
                stack.push(root.rightChild);
            if (root.leftChild != null)
                stack.push(root.leftChild);

        }
    }
}

4.4 MyBinaryTree.java

package tree;

public class MyBinaryTree<T> {
    MyTreeNode root = null;

    public MyBinaryTree(T data) {
        MyTreeNode<T> myTreeNode = new MyTreeNode<>();
        this.root = myTreeNode;
        this.root.data = data;
    }

    public MyBinaryTree() {
        MyTreeNode<T> myTreeNode = new MyTreeNode<>();
        this.root = myTreeNode;
        this.root.data = null;
    }

    public void createBinaryTree(T[] dataArray, MyTreeNode root) {
        StackToQueue<MyTreeNode> queue = new StackToQueue();
        this.root.data=dataArray[0];
        MyTreeNode parent;
        queue.push(root);
        for (int i = 0; i < dataArray.length / 2; i++) {
            parent = queue.pop();
            parent.addLeftChild(dataArray[2*i+1]);
            queue.push(parent.leftChild);
            parent.addRightChild(dataArray[2*i+2]);
            queue.push(parent.rightChild);
        }


    }


    public void beforeOrder() {
        root.beforeOrder(root);
    }

    public void preOrder(){
        root.preOrder(root);
    }

    public void middleOrder() {
        root.middleOrder(root);
    }

    public void inOrder(){
        root.inOrder(root);
    }

    public void behindOrder() {
        root.behindOrder(root);
    }

    public void afterOrder(){
        root.afterOrder(root);
    }

    public void breadthOrder() {
        try {
            root.breadthOrder(root);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }

    public void deepthOrder() {
        root.deepthOrder(root);
    }


}

写在最后

欢迎大家关注鄙人的公众号【麦田里的守望者zhg】，让我们一起成长，谢谢。